The day the Chinese puzzles took over
I’m really furious when people don’t bother to look for the original source of whatever they’re posting on the Internet (I feel I have a duty). I’m also angry at how many people are using reddit or sometimes Quora to ask questions that should have been posted on Stack Exchange or on specialized forums. The world is never going to fall short on reddittards…
Here’s a puzzle posted on reddit, allegedly “found out in the wild“:
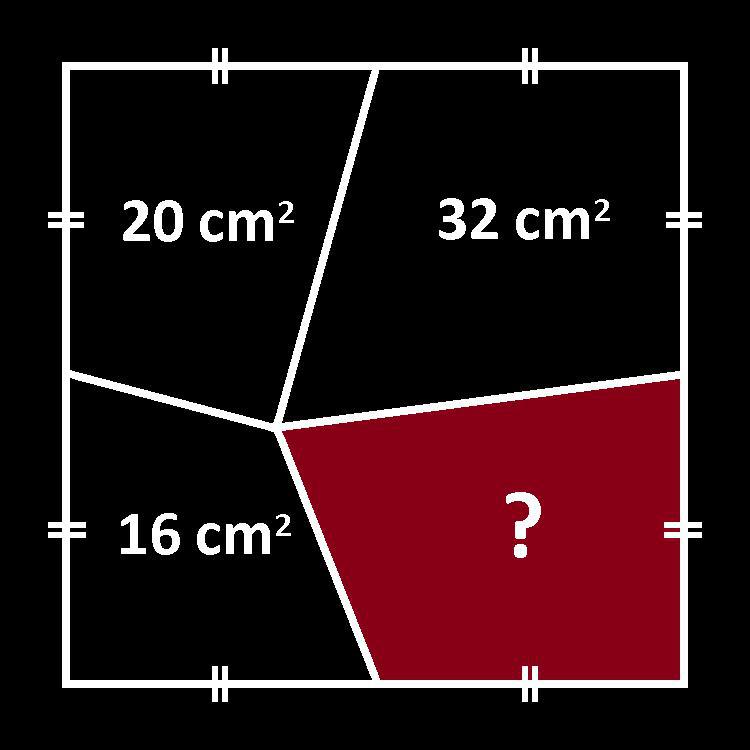
Greg Ross thought it a pretty puzzle. John Golden started a thread on Twitter about it. Oh, and nobody ever knew where the puzzle originated!
Of course it’s a nice one, especially as it’s supposed to be solved in a simple way. But heck, where does it came from?
It started on Weibo, then it showed up on the Russian blog Yandex Zen, on October 23, 2018; reposted on ChinesePlus.ru:
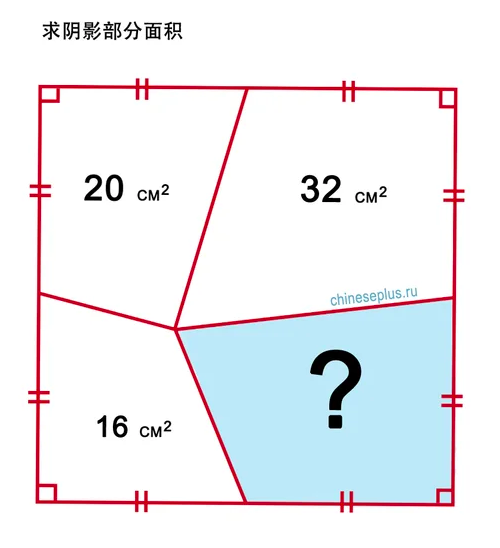
Apparently, it was a task for primary school in China, some say for the 4th grade! On October 29, the “official” solution–with a visual approach.
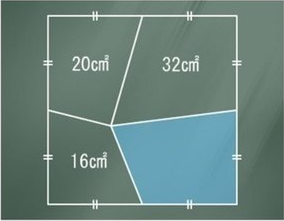
In the meantime, the puzzle also showed up on another Russian site, where it was later duplicated.
Is it really that difficult to search in the 21st century Internet? Are people lazy, stupid, careless, or (did I mention it?) just stupid?
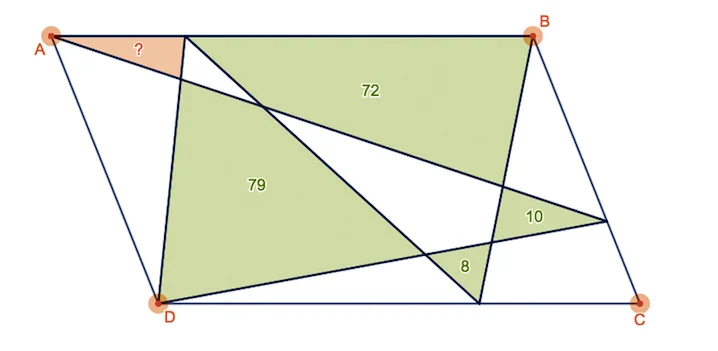
And here’s a derived puzzle:
Now, since you’re smarter than them, here’s some bonus puzzles of Sino-Russian descent–also geometrical.
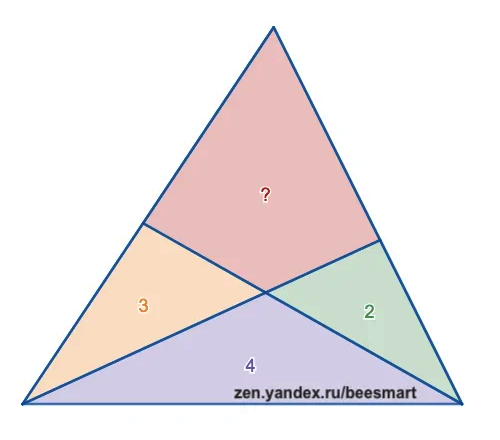
For the 5th grade: find the area of the pink triangle (posted here, then here; also here):
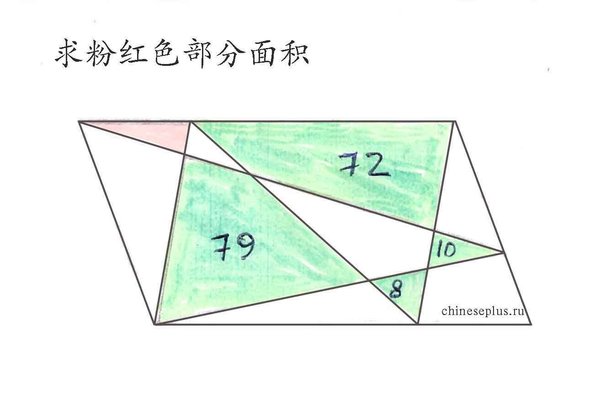
Visual solution here.
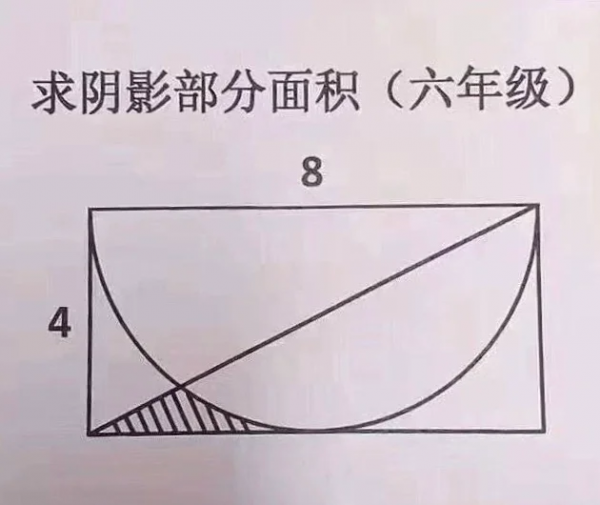
For grades 7-8 (google for it, it’s far from being original, or Chinese for that matter):
5th grade, to be solved mentally–find the area of the dark parts of the square:

6th grade, find the area of the shaded part:
A superb one–find the area of the rectangle:
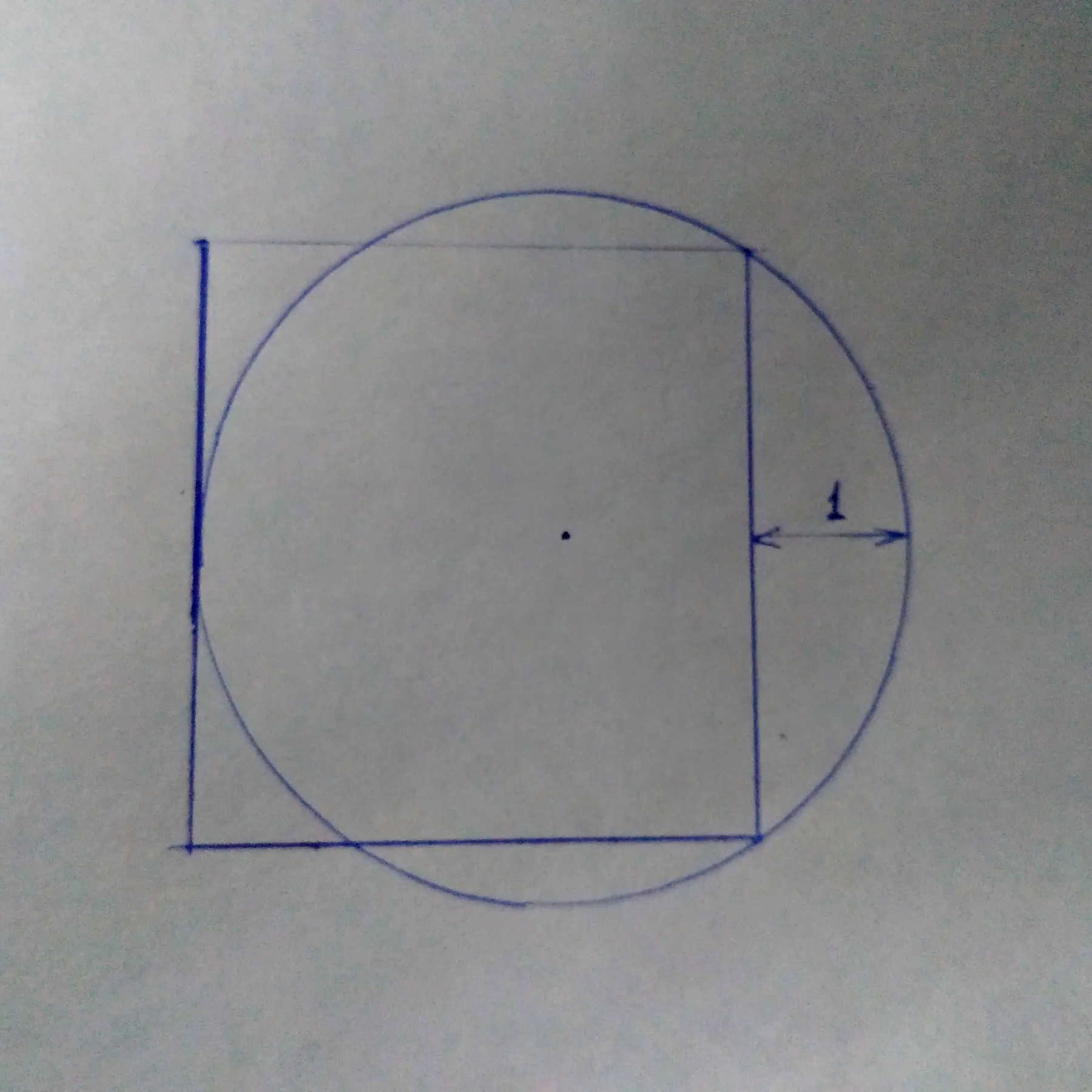
The answer is 16, and here’s why.
I’ll end with a personal correction to their opinion. Take this problem, where everything is in the picture (nothing is left out), and the question is: what is the area of the shaded area?
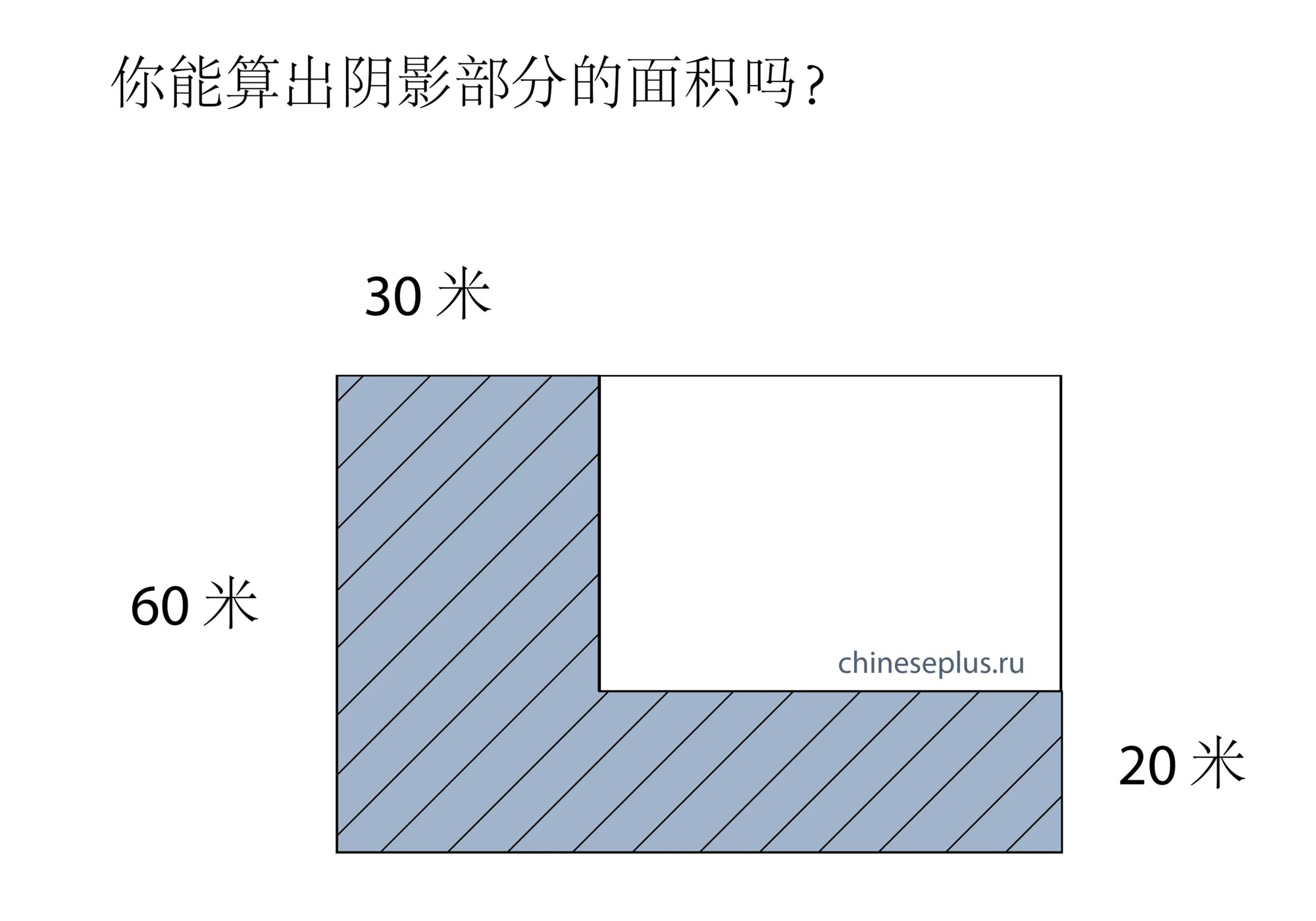
They argue that with what’s given there’s no numeric answer, so that “1800+20*X” is all that can be said:
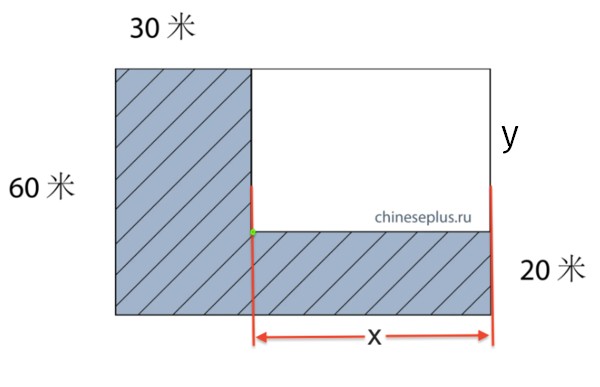
And yet… as long as this is for the elementary school, every single pupil would assume that the two rectangles are (as suggested graphically), similar. Therefore, (30+x)/x=60/y where y=40, hence x=60. The big rectangle is 90*60, the small one 60*40, and the shaded area is indeed 3000, as many people said.
FOLLOW-UP: I failed to follow Alex Bellos’s Monday puzzle column, but Greg Ross also discovered her: a math teacher fan of geometrical puzzles who posts them on Twitter: Catriona Shearer.
What made Alex and Greg click was an older one, mentioned by Alex on Jan. 14: Can you solve it? Catriona’s colourful conundrums.
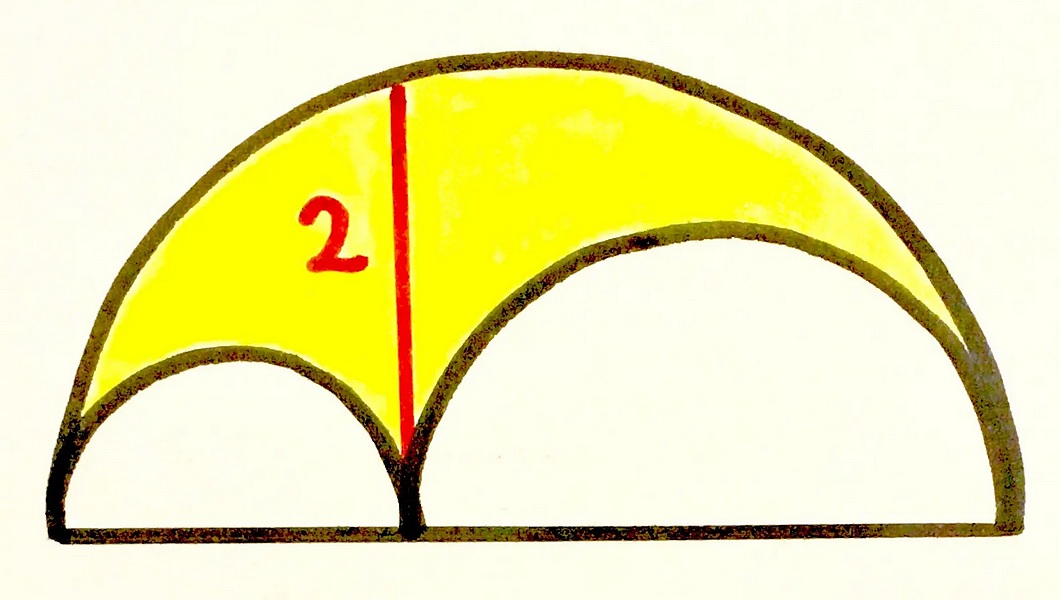
Other puzzles include:
Of course, there are many other people on Twitter to post geometrical puzzles:
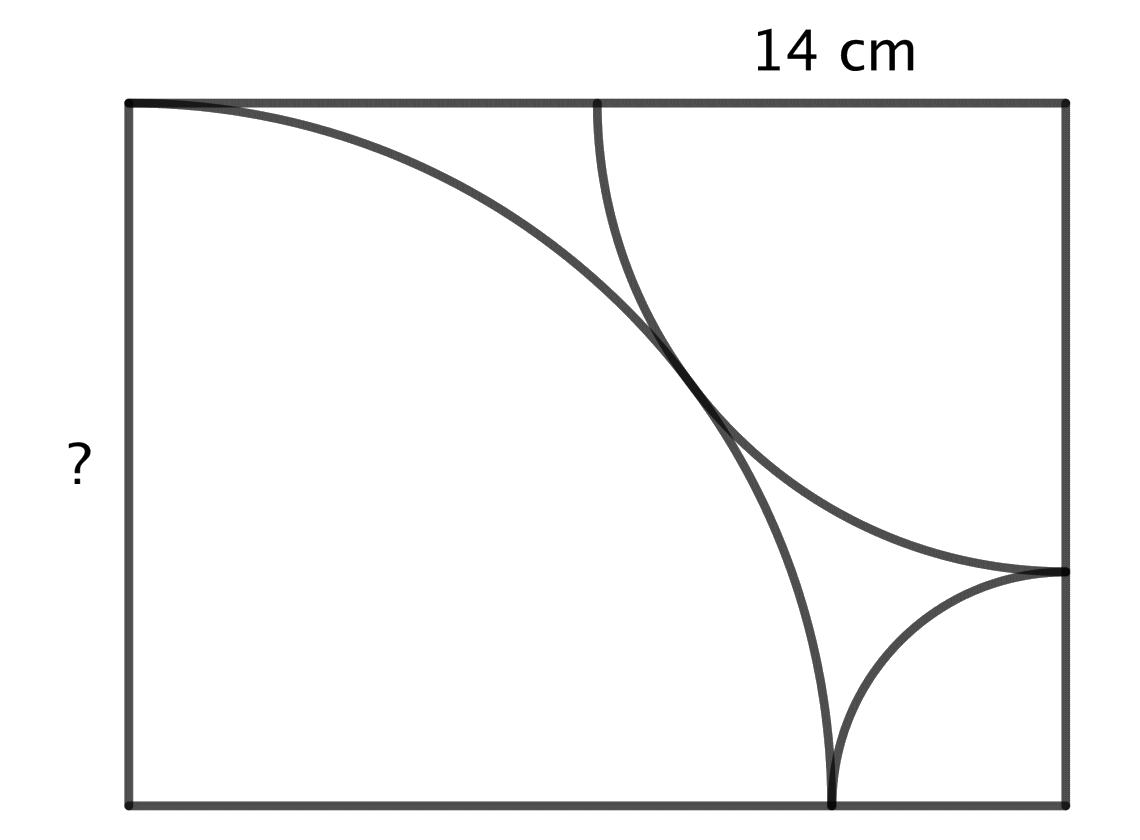
Now, a puzzle from a set of German puzzles dated 1967:
Back to Twitter, this reminded me that I own this book in print–15 euros is a bargain!
More of Catriona Shearer’s:
I’m not sure when did she post the following one; I’ve got it from Chalkdust:

JULY 5 UPDATE: It seems I forgot to mention Ed Southall. Take the following problem:
Elementary as it is, if you read the thread on Twitter, you’ll notice several approaches, solutions and attempted solutions (with the correct result, but questionable proof). I liked the “traditional” approach of “Geometry Dad” and the symmetry-based one of Uttam Grandhi.
Ed has many more puzzles on his blog, but I couldn’t manage to find the original blog or Twitter post for this one.

Added puzzles mostly from Catriona Shearer’s Twitter feed.
Catriona Shearer seems to have inspired other people, such as Diego Rattaggi, whose puzzles on Twitter are tagged #mathiratti.