The extra information meant he didn’t know she didn’t know…
Alex Bellos’s Monday puzzle in The Guardian online is something I once used to follow for a while, until the entire thing pissed me off too much. He’s no such thing as Henry Dudeney, Sam Loyd, Lewis Carroll, Raymond Smullyan, or Martin Gardner, but he wrote six books I know of, and he’s got a certain talent: the art of explaining smart puzzles poorly!
§1. Why Oxford is not the place to be
What bothers me with Alex Bellos is that he explains some of the puzzles he has shown absolutely infuriatingly. When the wording of the puzzle is very precise, the solution must be accurate too. When each verb, each noun and each adjective is carefully chosen to give the exact meaning that makes the puzzle difficult, sometimes deceiving, and frequently frustrating, the solution should be rigorously defined too.
There is a class of problems that go this way: some people are shown with partial information about something, and they’re told to infer from what they know the missing info. And then…
- Person 1: I know I don’t know the answer, but I also know that Person 2 doesn’t know the answer either.
- Person 2: Now that Person 1 has just said that, I know the answer!
- Person 1: Well, in that case, I know the answer too!
Maddening, right? To get a grip of how this might happen, you might want to consider some simpler cases, such as the many “colored hats” puzzles, of which I’d mention the most known ones.

In these puzzles, the fact that nobody says they know their own hat’s color allows someone to deduce the color of their own hat, and then the revealing process starts:
H1. The “2+2 hats and a wall, and they can only look forward”: e.g. here, here, here. Extremely popular and a bit dumb.
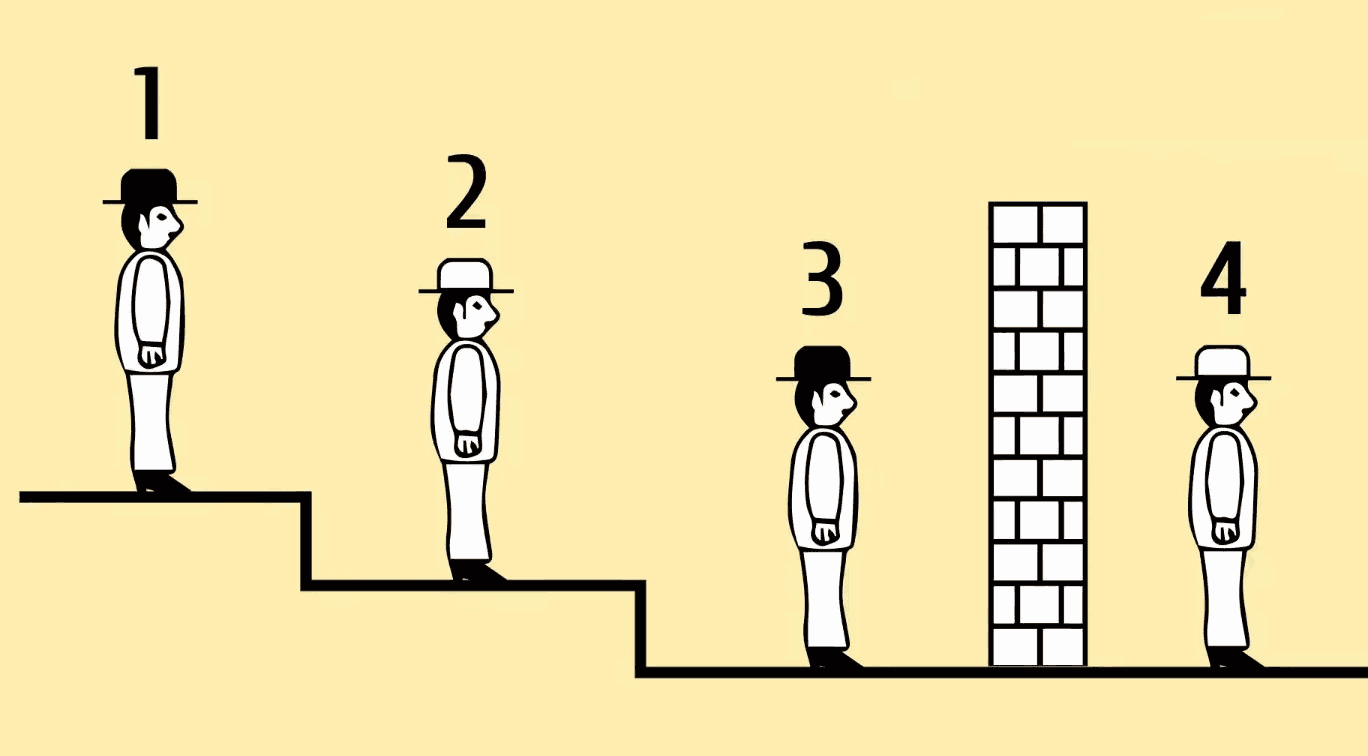
H2. The “3 hats that prove to be of the same color” aka The King’s Wise Men Hat Puzzle, which I don’t like at all, especially in the version with prerequisites such as:
- at least one of them is wearing a hat of a specified color;
- the contest is be fair to all three men (absolutely idiotic, and actually useless, as there’s a solution even in the absence of this “rule”).
The equivalent version told by Martin Gardner in The Second SciAm Book of Mathematical Puzzles and Diversions is much better though, and it carries no prerequisites:
Three men – A, B and C – are blindfolded and told that either a red or a green hat will be placed on each of them. After this is done, the blindfolds are removed; the men are asked to raise a hand if they see a red hat, and to leave the room as soon as they are sure of the color of their own hat. All three hats happen to be red, so all three men raise a hand. Several minutes go by until C, who is more astute than the others, leaves the room. How did he deduce the color of his hat?
C asks himself: Can my hat be green? If so, then A will know immediately that he has a red hat for only a red hat on his head would cause B to lift his hand. A would therefore leave the room. B would reason the same way and also leave. Since neither has left, C deduces that his own hat must be red.
H3. The “3 hats out of a set of 3+2”, as formulated by MIT mathematician Tanya Khovanova:
Three logicians walk into a bar. Each is wearing a hat that’s either red or blue. Each logician knows that the hats were drawn from a set of three red and two blue hats; she doesn’t know the color of her own hat, but can see those of her companions.
The waiter asks, “Do you know the color of your own hat?”
The first logician answers, “I do not know.”
The second logician answers, “I do not know.”
The third logician answers, “Yes.”
What is the color of the third logician’s hat?
H4. The “3 hats out of a set of 3+2 , and they can only look forward,“ as brilliantly explained here (only one prisoner’s hat color can be deduced). Popular Mechanics featured the same puzzle.
H5. The “3 hats of colors 2+1 or 1+2, and they can only look forward” as described e.g. here in Variant 1.

That’s much simpler, because no matter the color, all 3 can’t be the same. When C could not guess, B knew that he and A were wearing different colors of caps, otherwise C would have known his color was the other one. Since B also couldn’t guess, while knowing what should have been the reasoning of C (they’re all perfect logicians!), it goes this way: B should wear the color that A isn’t wearing, in our case B knows he’s wearing Red, because he can see that A is wearing Blue. Once B announces the color of his cap, A also knows his color, but due to the “2+1 or 1+2” rule, C remains unable to guess.
H6. The ten prisoners, nine of which must guess correctly. That’s a much tougher variation in which some lateral thinking is required: on YT here. Or the 100 prisoners, 99 of which must guess correctly, on YT here, and also on Popular Mechanics. Apparently, Google used that puzzle in their recruitment interviews, and there was an AI study on that (read more about the context).

Back to Alex Bellos and his column. The July 12 set of puzzles, all of which were “set in recent years during Oxford university admissions interviews for joint philosophy degrees,” included this one:
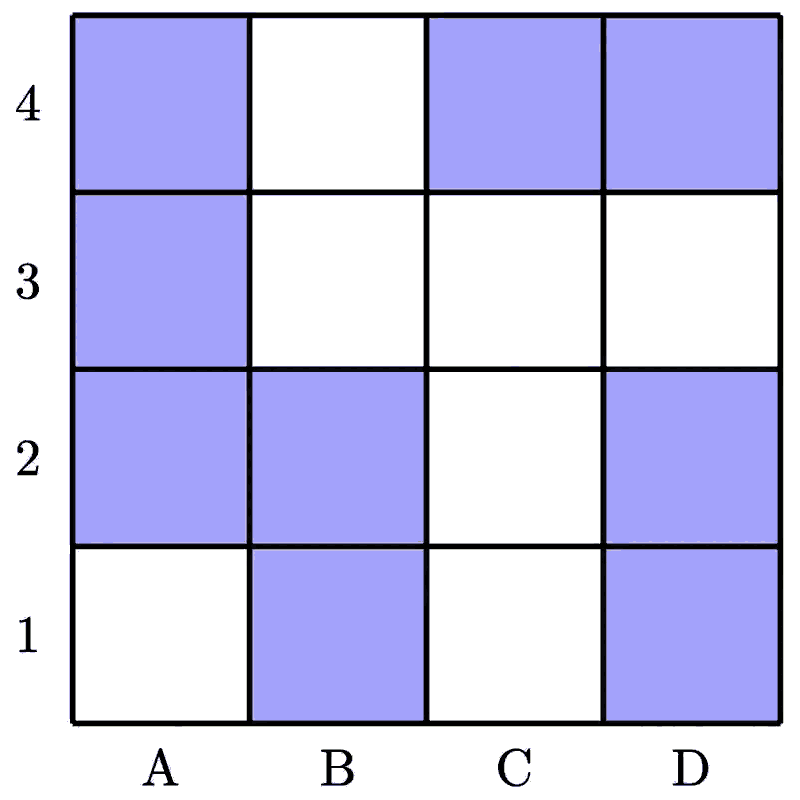
Stephanie’s surprise
Stephanie has invited her friends Rowan and Colleen to her home. They are all perfectly logical. She tells them that she has hidden a surprise under one of the blue squares.
Stephanie has privately told Rowan the row number of the surprise and Colleen the column letter of the surprise, and everyone is aware of this. The following conversation ensues.
Rowan: I don’t know where the surprise is, but I also know that Colleen doesn’t know.
Colleen: Yes, indeed, at first I didn’t know the location of the surprise. But now I know where it is.
Rowan: In that case, I now also know where it must be.
Question. Where is the surprise?
There is a follow-up, but I’m leaving it for later.
The presented solution is terribly succinct:
Solution: Under square A2.
If Rowan doesn’t know where the surprise is we can eliminate row 3 (since if he was told row 3 he would know the correct square.) If he knows that Colleen doesn’t know, we can eliminate row 4 (since the only way it would be possible for Colleen to know the correct square at the start is if it was C4.) If Colleen now knows the correct square, she must know the column for which there is only one option left. This column is A, and thus the correct square is A2.
If you really want it now, here’s the follow-up…
Follow up: Suppose that before any conversation took place, someone trips over B1, which opens, revealing it to be empty. a) Could the conversation have proceeded as before? b) Were either of them surprised to see it empty? c) How can it have changed the conversation, if they both knew it already. d) How can it be that adding information, that B1 is empty, makes Rowan’s statement become false? (This is the most interesting aspect of the puzzle, since it seems paradoxical that adding information can reduce knowledge.)
…and the solution to it:
Follow up: a) No. The second part of Rowan’s first statement is now false. b) No. They both knew that B1 wasn’t the tile. c) Because they are learning knowledge about knowledge. d) The knowledge that Rowan had was that Colleen didn’t know something – and the extra information gleaned meant that he lost that knowledge, because it meant he didn’t know she didn’t know. The extra information might have given her knowledge, for example, if it had been B2, she would have known after seeing B1 empty.
Crystal-clear is it… not.

This is when normally I get angry. This time, I felt a bit like these guys from the comments section:
Antidote2: I do not get the second claim in the solution to puzzle 1. If Colleen doesn’t know the solution, surely this invalidates column C and not row 4 i.e. A4 and D4 are possible sites. Leaving an unsoluble situation without further information?
ChristopherCundiff: I had trouble with that too. I was thinking that her comment meant only that she could rule out C4, not the whole of row 4.
Theshortestone: Surely if Rowan knew the surprise was in row 4 then he could be confident that Colleen didn’t know as it could be under either A4 or D4…
I must be missing something very basic.
As for the follow-up…
ChristopherCundiff: I thought I was Beginning to Understand the Answer. Then I got to… “Rowan knew that Colleen didn’t know something – and the extra information gleaned meant that he lost that knowledge, because it meant he didn’t know she didn’t know…”
And you know what? The best explanation came from this other guy, in several installments that I joined here:
abcxyz987: Let’s unwrap what Rowan says “I don’t know where the surprise is, but I also know that Colleen doesn’t know.”
“I don’t know where the surprise is” means that it can’t be row 3.
Now “I also know that Colleen doesn’t know.” means that Rowan knows that Colleen doesn’t know. If Rowan had been told that the surprise is in row 4, then he couldn’t have confidently said that he knows that Colleen doesn’t know. This means that it can’t be row 4.
Now, Colleen says: “Yes, indeed, at first I didn’t know the location of the surprise. But now I know where it is.”
The first part is vacuous. She’s simply confirming what Rowan knew. However, based on what Rowan has said, she can work out (as we have worked out) that the surprise cannot be in rows 3 and 4.Given this information she concludes: “But now I know where it is.” If she know knows where it is, then it must be A2, because if she had been told columns B and D, then she would not have had enough information to come to a conclusion and we already know that it couldn’t have been column C. Therefore it must be column A, which only has one box in rows 1 and 2.
If Rowan knew that it was in row 4, he couldn’t have been confident that for sure Colleen didn’t know it. The only thing he could conclude was that maybe Colleen did know it (if it was C4) or maybe Colleen didn’t know it (if it was A4 or D4).
Just to paraphrase, if Rowan knew it was row 4, he could not have said “I also know that Colleen doesn’t know.” He could only have said “I do not know whether Colleen knows or not.” Or “I cannot decide whether Colleen knows or not.”

I have several problems with the original puzzle’s wording and its solution. OK, they cared to mention that “They are all perfectly logical,” however:
- It’s nowhere said whether anyone who knows where the surprise is should speak out first, right away, or at all.
- Therefore, if Colleen didn’t speak yet, the most reasonable assumption is that she wasn’t told column C, so she can’t know right away, and she might still be thinking.
- But… hold on! If she had been told column C, or if Rowan had been told row 3, there wouldn’t have been any puzzle at all! Isn’t it therefore safe to assume that Colleen couldn’t have been told column C, and Rowan couldn’t have been told row 3?
- The answer to the above question has its importance, as interpreting Rowan’s “I also know that Colleen doesn’t know” to imply “we can eliminate row 4” is a bit far-fetched. He did not say “I also know that Colleen CAN’T POSSIBLY KNOW,” which is the only way to express a statement to the effect that the surprise can’t be in row 4. Simply stating “I know that Colleen doesn’t know” only means that she remained silent, and the only certain thing to be deduced is that she hasn’t been told column C (if that was ever a choice, that is)!
It’s a matter of wording. The nitpicker in me considers that, semantically (and therefore logically), there’s a huge difference between the two following statements:
- someone doesn’t know
- someone can’t possibly know
This should have been reflected in the wording of the puzzle, and it wasn’t.

You’re free to disagree with me, but wording is extremely important. Take a look in the same column at Numbers in New Guinea (it’s numbing). Take a look at The Hardest Logic Puzzle Ever. Even when words have other meaning than the expected one (like in those tests with GREEN written in red, and RED written in blue), the pivot to our reasoning is the word.
I know from Martin Gardner (see Chapter Nineteen of The Second SciAm Book of Mathematical Puzzles and Diversions) the so-called Bertrand’s problem (you can read a bit on Wikipedia too), and notice how ambiguous this wording is:
choose a chord of the circle at random
How exactly are you making this “random” choice?
- You choose two random points on the circle and join them. (Answer: 1/3.)
- You choose a radius of the circle, choose a point on that radius, and draw a chord through that point that’s perpendicular to the radius. (Answer: 1/2.)
- You choose a radius of the circle, choose a point on that radius, and draw a chord through that point at a random angle.
- Choose a point anywhere in the circle and draw the chord for which this is the midpoint. (Answer: 1/4.)
- Choose a point anywhere in the circle and draw a chord through it at a random angle with the horizontal.
They all are random, and yet…

As for how gaining extra information can mean you actually lose some information…
§2. What’s puzzling me about today’s puzzle
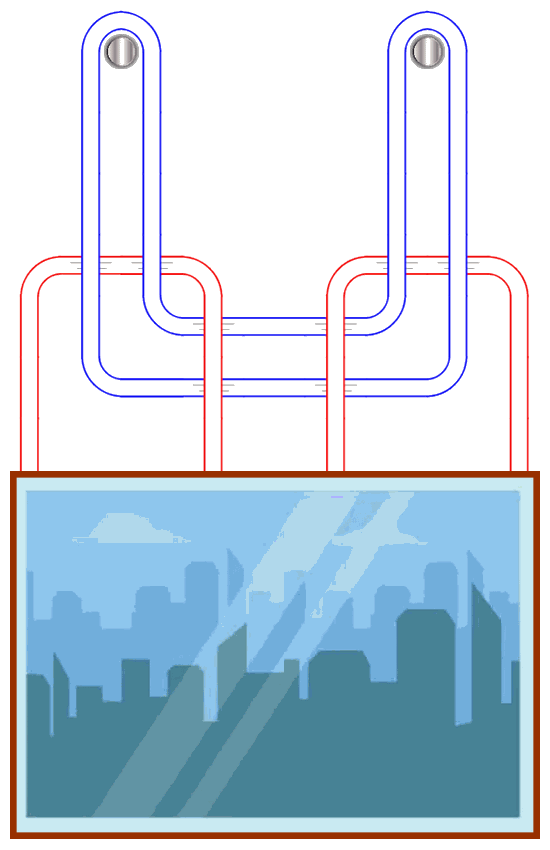
Today, it started with The magic of the Borromean rings, only to introduce the classic Picture-Hanging Puzzle:
To push towards a Boromean-esque solution, he hinted to it:
Can you think of a way to hang a picture on a wall using string and two nails, such that if either of the nails fails (and the other one doesn’t) then the picture will fall to the floor?
This is a puzzle that is quite hard to visualise, so I would recommend playing around with nails and a piece of string. If you don’t have any nails at hand, maybe use some rings.
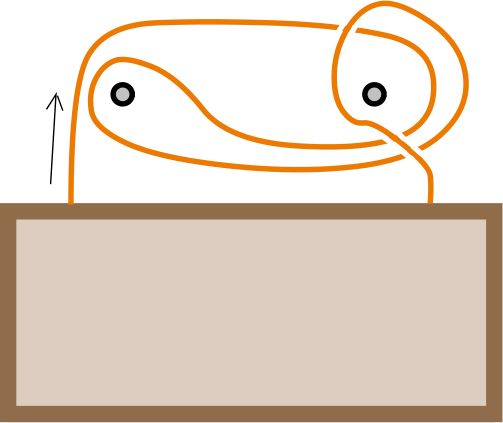
The “orthodox” solution is part of the official solution page, but then there’s also another one. The one I called “orthodox” (arXiv:1203.3602) has the merit of being generalizable to more than two nails. (See also an improvement: arXiv:2102.00984; and doi.org/10.1016/j.promfg.2018.03.149.)
The “orthodox” solution can be drawn in several ways:

Alex Bellos showed the “improved” one first, for which again I’ll show you a slightly different drawing:
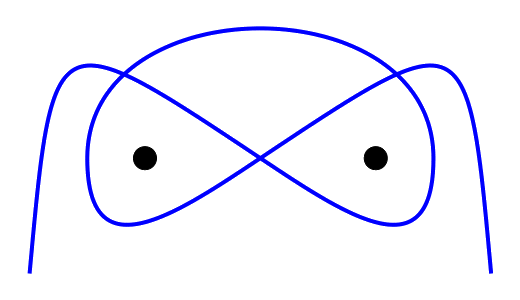
There are also two more similar solutions. And a quite ingenious one, if and only if the proposed way of attaching is allowed (which doesn’t seem to be the case):
One nail in the wall with one end of the string attached to it. The other nail in the picture with the other end of the string attached to it. Either nail fails, the picture falls.
Why am I slightly frustrated then? One more time, the WORDING!
His problem was worded in a way that only declared a fixed number of pins, but the string was NOT limited to a unique, long piece!
using string and two nails
So what bothers me is that nobody seems to have thought of a solution involving several pieces of string, which is what occurred to me in the first place as the simplest one to imagine! (I used KnotMaker for the drawing.)
Well, I’ll take a break from Alex Bellos’ column for another (long) while. Should I want to read him, I can resort to the following books of his, in ePub format:
- Alex’s Adventures in Numberland (2010)
- The Grapes of Math (2014)
- Can You Solve My Problems (2016)
- So You Think You’ve Got Problems (2019)
- Perilous Problems for Puzzle Lovers (2020)
- The Language Lover’s Puzzle Book (2020)
They’re far from being the best in the known Universe, so the backlog of books with logic puzzles is huge. Maybe in a future lockdown…

Leave a Reply