Nicușor Dan și rezolvarea din 2020 a problemei din 1988

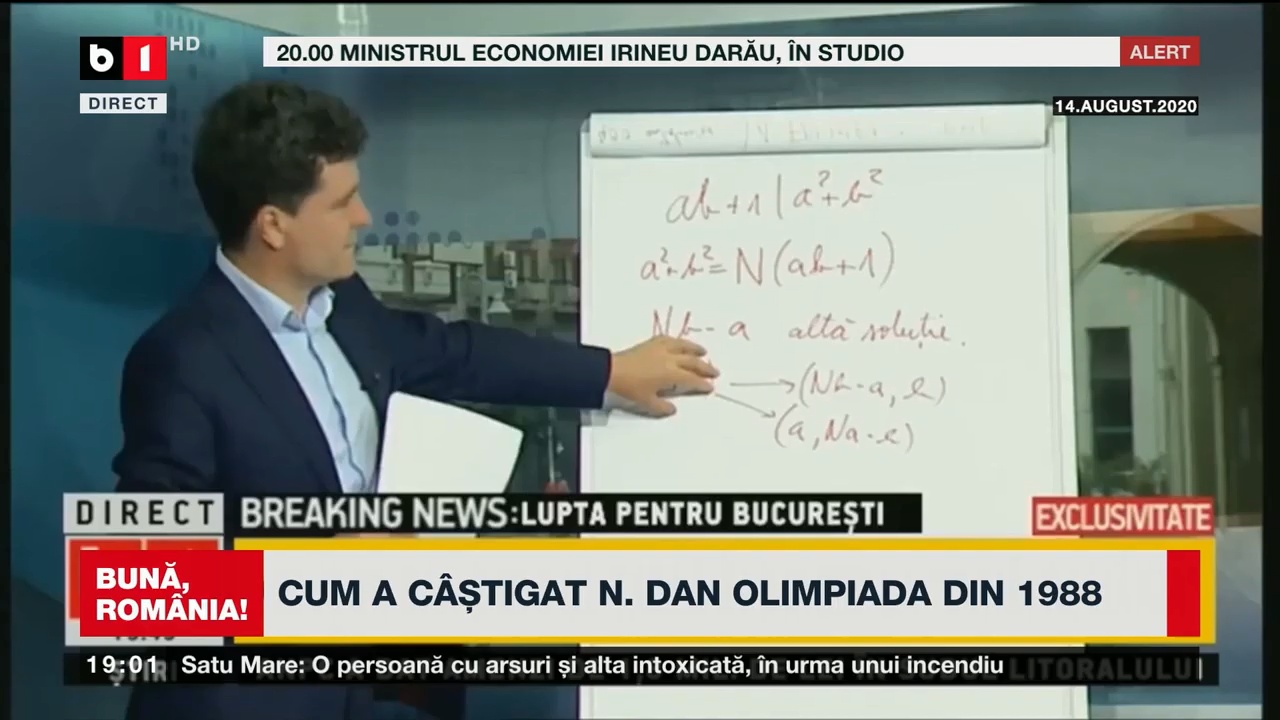
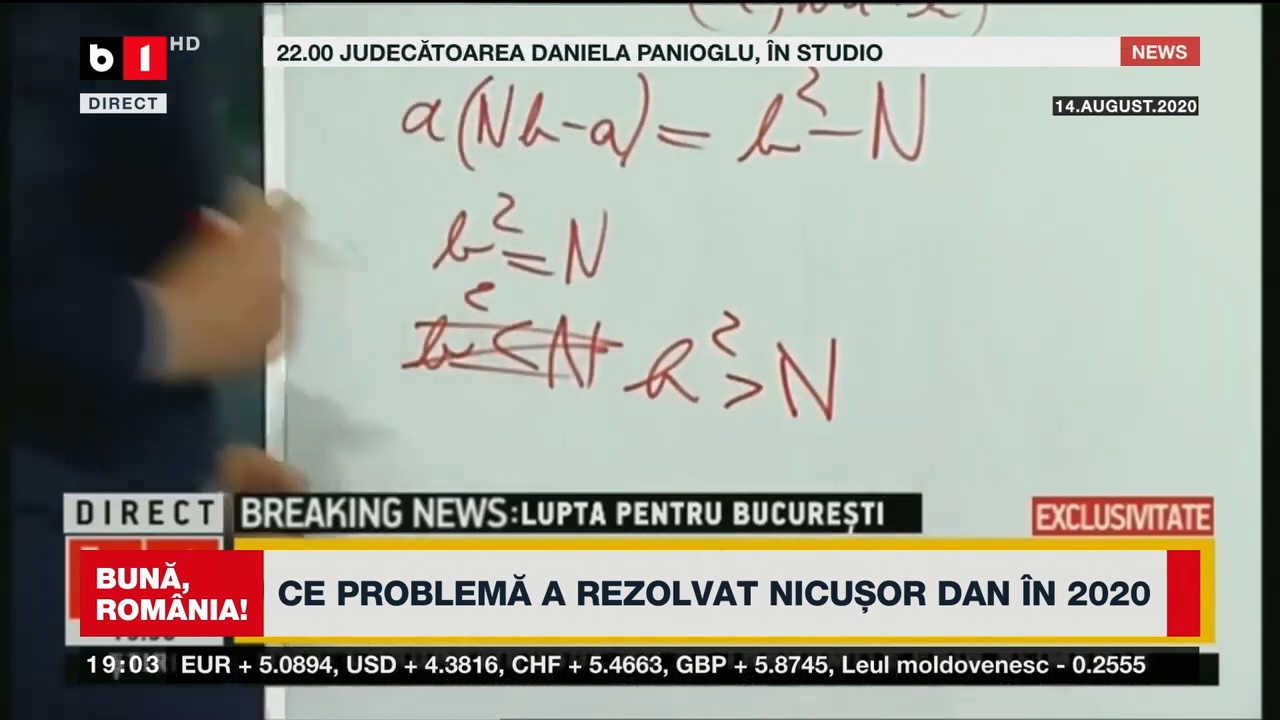
Nu am avut timp să „sap” mai mult, iar gradul în care-mi mai amintesc matematica de acum 35+ ani este modest, însă am aflat că s-a discutat din nou problema de la olimpiada de matematică din 1988 pe care Nicușor Dan a rezolvat-o (dacă putem considera că a făcut-o cu adevărat) în ziua de 14 august 2020, în direct, la B1 TV. Contextul este acela în care un profesor se lăuda cu o generalizare.

Puteți găsi rezolvarea în emisiunea „Bună, România!” din 16 ianuarie:

Hai să lămuresc întâi povestea profesorului Mihai Teodor, tratată în aceeași emisiune: găsiți menționată contribuția acestuia în The On-Line Encyclopedia of Integer Sequences, sub codul A061076.

A061076
a(n) is the sum of the products of the digits of all the numbers from 1 to n.

1, 3, 6, 10, 15, 21, 28, 36, 45, 45, 46, 48, 51, 55, 60, 66, 73, 81, 90, 90, 92, 96, 102, 110, 120, 132, 146, 162, 180, 180, 183, 189, 198, 210, 225, 243, 264, 288, 315, 315, 319, 327, 339, 355, 375, 399, 427, 459, 495, 495, 500, 510, 525, 545, 570, 600, 635

COMMENTS
...
For n = 10^(k-1), the closed-form formula from Mihai Teodor (see Formula section) gives a(n) = (45^k - 45)/44, so lim_{n->oo} log(a(n))/log_10(n) = log(45) = 3.80666248977.... - Jon E. Schoenfield, Apr 10 2022
...
FORMULA
...
Let b(1), b(2), ..., b(k) be the digits of the base-10 expansion of n: n = b(1)*10^(k-1) + b(2)*10^(k-2) + ... + b(k). Then a(n) = b(1)*b(2)*...*b(k) + (45^k-45)/44 + (1/2)*Sum_{i=1..k} b(1)*b(2)*...*b(i)*(b(i)-1)*45^(k-i). - Mihai Teodor, Apr 09 2022

Nu are prea mult de-a face cu rezolvarea problemei „noastre”.

Pe situl International Mathematical Olympiad găsiți, prin căutări judicioase, problema a șasea din a doua zi a olimpiadei din 1988 care s-a ținut la Canberra:

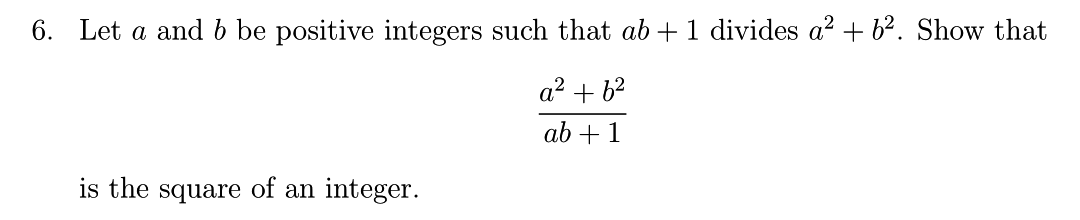
Mai găsiți și rezultatele echipei române.

Nu am găsit vreo soluție oficială.

Cu privire la „prestația” din 2020 a lui Nicușor Dan, nu este prima oară când acesta este împrăștiat, varză, muci. Cu siguranță era mai organizat, mai sistematic, în școală și facultate, căci nivelul haotic în care-și prezintă astăzi soluțiile nu i-ar fi permit nici măcar să obțină notă de trecere în învățământul preuniversitar, darămite să câștige olimpiade și să ia examene de nivel universitar.

I-am cerut lui Kimi o soluție, iar răspunsul acestuia mi s-a părut ingenios. A halucinat numele autorului. Garantat problema nu a fost formulată de nici unul din cei doi Lebesgue: Henri Léon Lebesgue, cunoscut pentru teoria integrării, sau mai puțin cunoscutul Victor-Amédée Lebesgue, cu contribuții în teoria numerelor. În al doilea răspuns, Kimi a precizat însă că „Problema originală a fost propusă la Olimpiada Internațională de Matematică din 1988 (IMO 1988).”

Enunțul meu pentru Kimi:

Fie 2 numere pozitive, a și b, astfel încât ab+1 | a²+b²
Să se demonstreze că (a²+b²)/(ab+1) este pătrat perfect.

Dacă nu cumva are vreo scăpare de logică, soluția lui Kimi mi se pare elegantă:

Voi demonstra că raportul $\frac{a^2 + b^2}{ab + 1}$ este într-adevăr un pătrat perfect, folosind metoda descenței infinite a lui Vieta jumping.

---

Pasul 1: Reformulăm problema

Fie $k = \frac{a^2 + b^2}{ab + 1}$. Dorim să demonstrăm că $k$ este un pătrat perfect.

Observăm că $k$ este un număr întreg pozitiv, deoarece $ab + 1$ divide $a^2 + b^2$.

---

Pasul 2: Presupunem că $k$ nu este pătrat perfect

Vom folosi metoda reducerii la absurd. Presupunem că există o pereche $(a, b)$ de numere pozitive astfel încât $k = \frac{a^2 + b^2}{ab + 1}$ nu este pătrat perfect.

Fără a pierde generalitatea, presupunem $a \geq b$.

---

Pasul 3: Construim o soluție mai mică

Considerăm ecuația în $x$:

$x^2 – k b x + (b^2 – k) = 0$

Observăm că $x = a$ este o soluție a acestei ecuații, deoarece:

$a^2 – k b a + (b^2 – k) = 0 \implies a^2 + b^2 = k(ab + 1)$

Fie $a_1$ cea de-a doua soluție a ecuației. Conform relațiilor lui Vieta:

$a + a_1 = k b \quad \text{și}\quad a a_1 = b^2 – k$

De aici obținem:

$a_1 = k b – a = \frac{b^2 – k}{a}$

Deoarece $a, b, k$ sunt întregi, rezultă că $a_1$ este și el întreg.

---

Pasul 4: Analizăm semnul lui $a_1$

Dacă $a_1 = 0$, atunci $b^2 = k$, deci $k$ este pătrat perfect, contradicție cu presupunerea noastră.

Dacă $a_1 < 0$, atunci:

$a_1 = \frac{b^2 – k}{a} < 0 \implies b^2 < k$

Dar $k = \frac{a^2 + b^2}{ab + 1} \leq \frac{a^2 + b^2}{ab} = \frac{a}{b} + \frac{b}{a} \leq \frac{a}{b} + 1$ (deoarece $a \geq b$)

Dacă $b^2 < k$, atunci $k > b^2$, ceea ce implică:

$\frac{a^2 + b^2}{ab + 1} > b^2 \implies a^2 + b^2 > b^2(ab + 1) \implies a^2 > ab^3$

Dar aceasta este imposibil pentru $a, b \geq 1$.

Prin urmare, $a_1 > 0$.

---

Pasul 5: Obținem o soluție mai mică

Am găsit o nouă pereche $(b, a_1)$ cu $a_1 > 0$ și:

$\frac{b^2 + a_1^2}{b a_1 + 1} = k$

Deoarece $a_1 = \frac{b^2 – k}{a} < \frac{b^2}{a} \leq b \leq a$, am obținut o soluție mai mică (în sensul că suma componentelor a scăzut).

---

Pasul 6: Aplicăm descendența infinită

Putem repeta acest proces indefinit, obținând soluții din ce în ce mai mici. Dar acest lucru este imposibil, deoarece numerele pozitive nu pot descrește la infinit.

Singura posibilitate este ca procesul să se oprească atunci când $a_1 = 0$, caz în care $k = b^2$, deci $k$ este pătrat perfect.

---

Concluzie:

Raportul $\frac{a^2 + b^2}{ab + 1}$ este întotdeauna un pătrat perfect.

Oricum, cei doi cetățeni de la „Bună, România!” (Radu Buzăianu și Răzvan Zamfir) nu au absolut deloc habar de matematică, astfel încât ar fi fost de preferat să bată mai puțin câmpii. Dacă l-ar fi chemat pe CTP ca să comenteze soluția, alta ar fi fost situația.