Nostalgia & Fun With Calculators
Despite having developed a dependency of my ~200 installed Android apps and ~150 installed Windows programs, I still use a hand-held scientific calculator. Most of the time I’m using it for innocuous tasks–making sense of the monthly expenses, which I categorize and track in time, for which the fact that such a calculator has a 2-display line is of a great help.
I’m actually using two calculators during the categorization of the expenses. To subtract items from a receipt while not interrupting what I’m doing with the physical calculator, I use an Android app. But I still need the first one! (I’m a person who likes to touch and to feel, hence I very much appreciate a physical object. I’m a person who wears a wristwatch to know the time.)
Speaking of apps: the stock Android calculator is an unusable piece of ugly crap; after having tried dozens of alternatives, I settled for the most convenient one: CalcTastic’s Scientific Calculator, the free and ad-free edition. The paid edition is worth the money if you need more themes and a programmer’s calculator layout, but I find the programmer’s approach much less practical than KebStudio’s BitCalculator.
The thing is, sometimes I remember that in high school and college I was able to do more, such as solving simple everyday questions by modeling them so that a simple integral calculus would provide the answer. But tell me how on Earth would you do that with a regular scientific calculator, being it physical or an app?

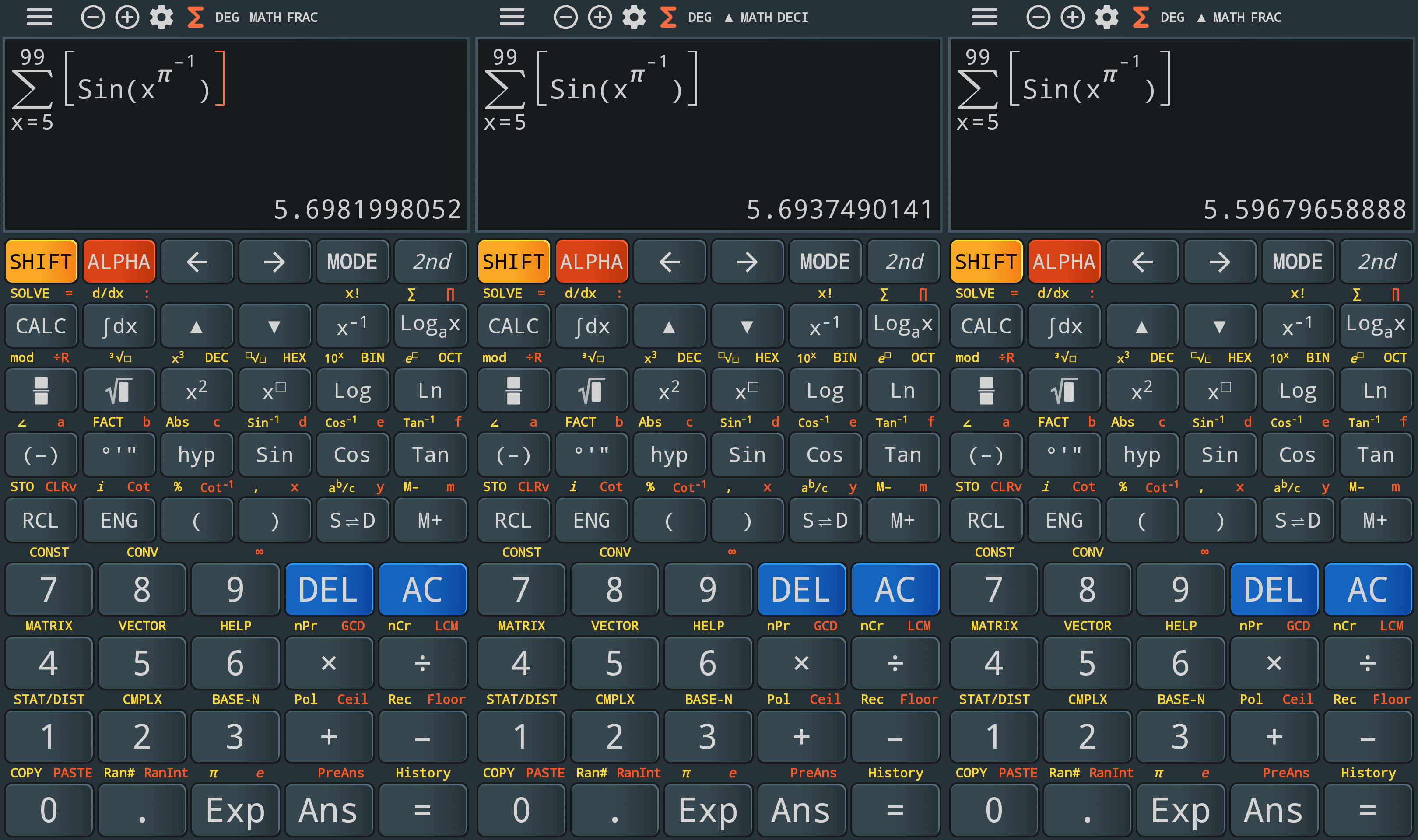
OK, the first one is actually a matter of symbolic calculus. It’s 4x when x=1, so it’s 4. But the second one… how do you so it? How do you enter it on your calculator?
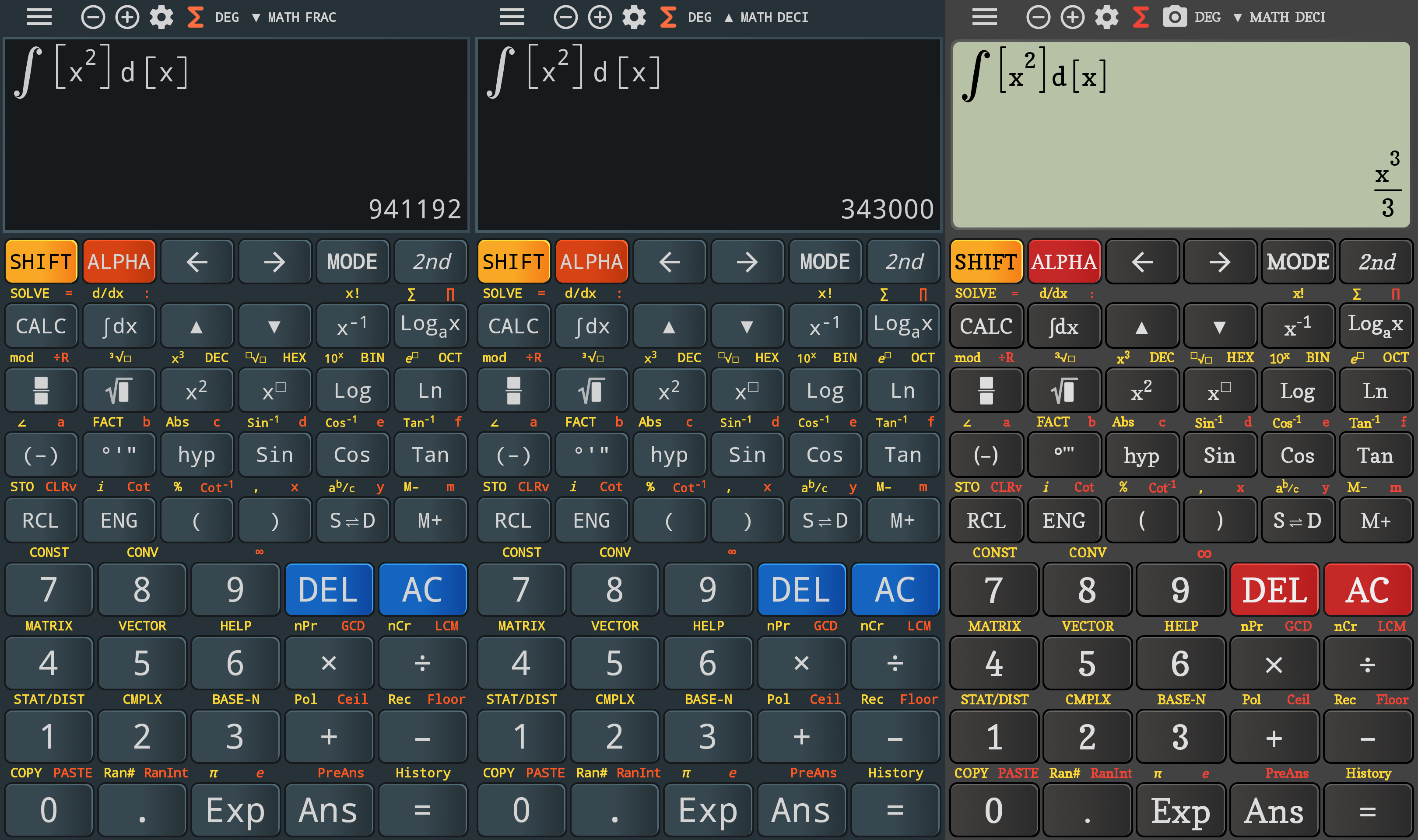
We’re not in the 1980s anymore, and the reference is not CASIO fx-82 anymore. Today we have matrix displays dubbed Natural Display, Natural Textbook Display, Visually Perfect Algebraic Method (V.P.A.M.) or Natural V.P.A.M.–the idea being that one can input formulas exactly as they are normally written on paper or in a textbook. And yet, most such calculators are used in K-12 to operate with fractions, to simplify them and to give results in fractions or generally in symbolic writing instead of numerical values, e.g. 2√2/3 instead of 0.942809041.

Now, simplifying fractions is an extremely dumb thing, but this makes Texas Instruments and CASIO sell quite a lot of devices to kids in the States. What’s worth the money is a device able to solve such things:

Of course, it can also display 0.5.
Notice however that this is a symbolic result that is “nice” enough to have a perfect precision. What happens when a calculator doesn’t solve the integral before computing it, but it actually use an approximation method, such as the Gauss–Kronrod quadrature formula? Let’s compare the fabulous CASIO fx-991EX ClassWiz with the ugly TI-36X PRO and with an Android app, Philip Stephens’ Scientific Calculator:

Wow. If the physical calculators agree on 7 significant digits (of which 4 decimals: 9281), the app is severely wrong: only 4 correct digits!
That’s because it doesn’t solve the integral. Let’s ask Wolfram Alpha:
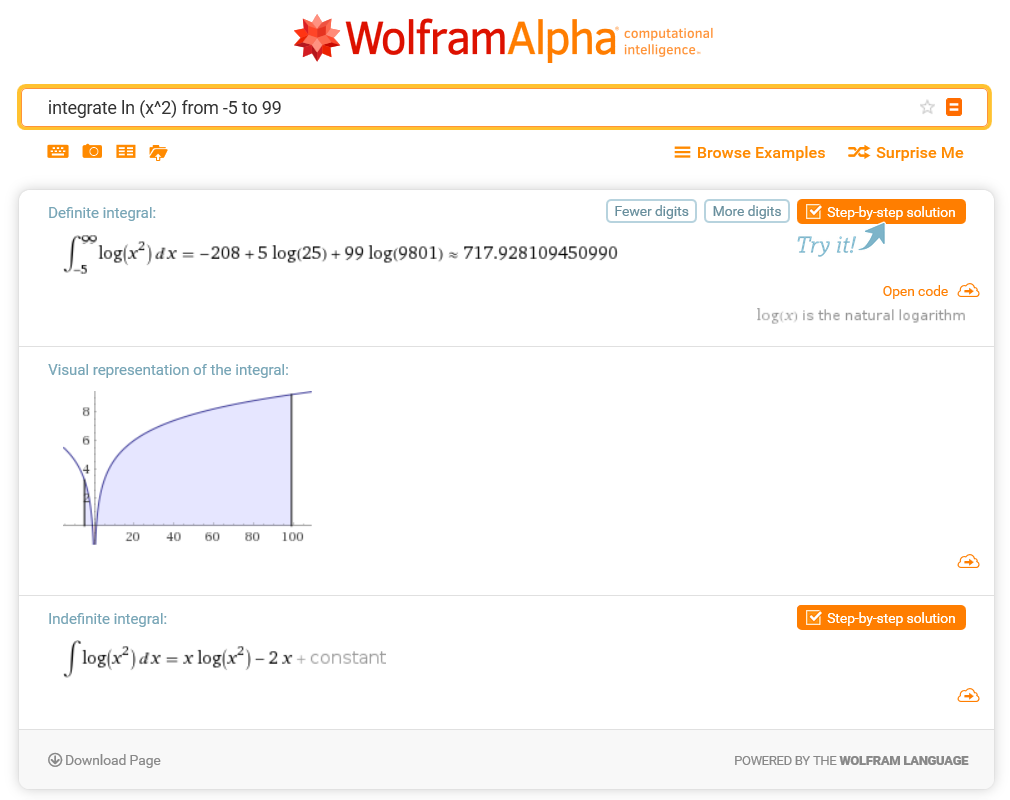
It solves it well, but it only gives 5 digits. Let’s compare the two ways of getting a numerical result (approximated vs. solved), and also ask CalcTastic about the value of the solved expression:
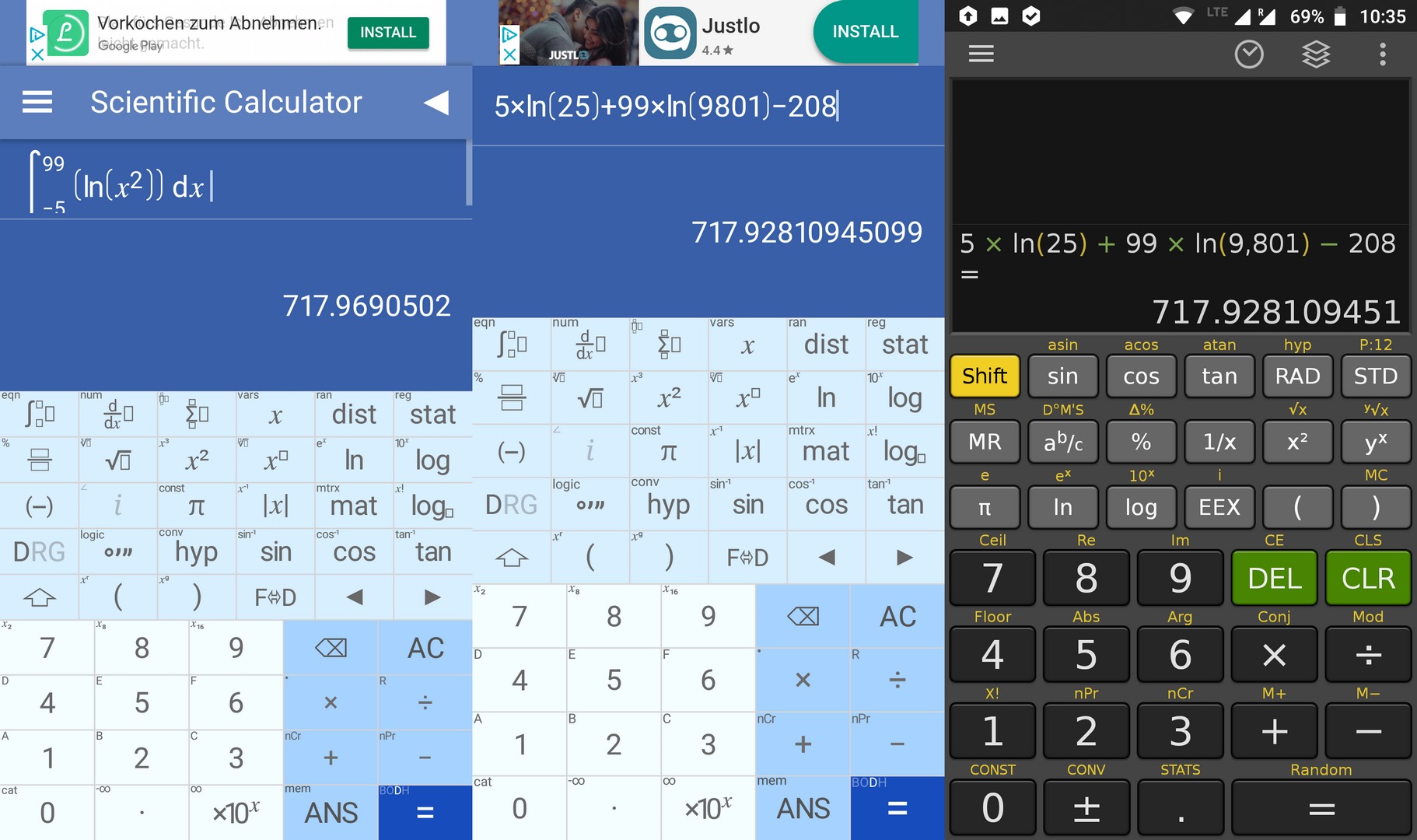
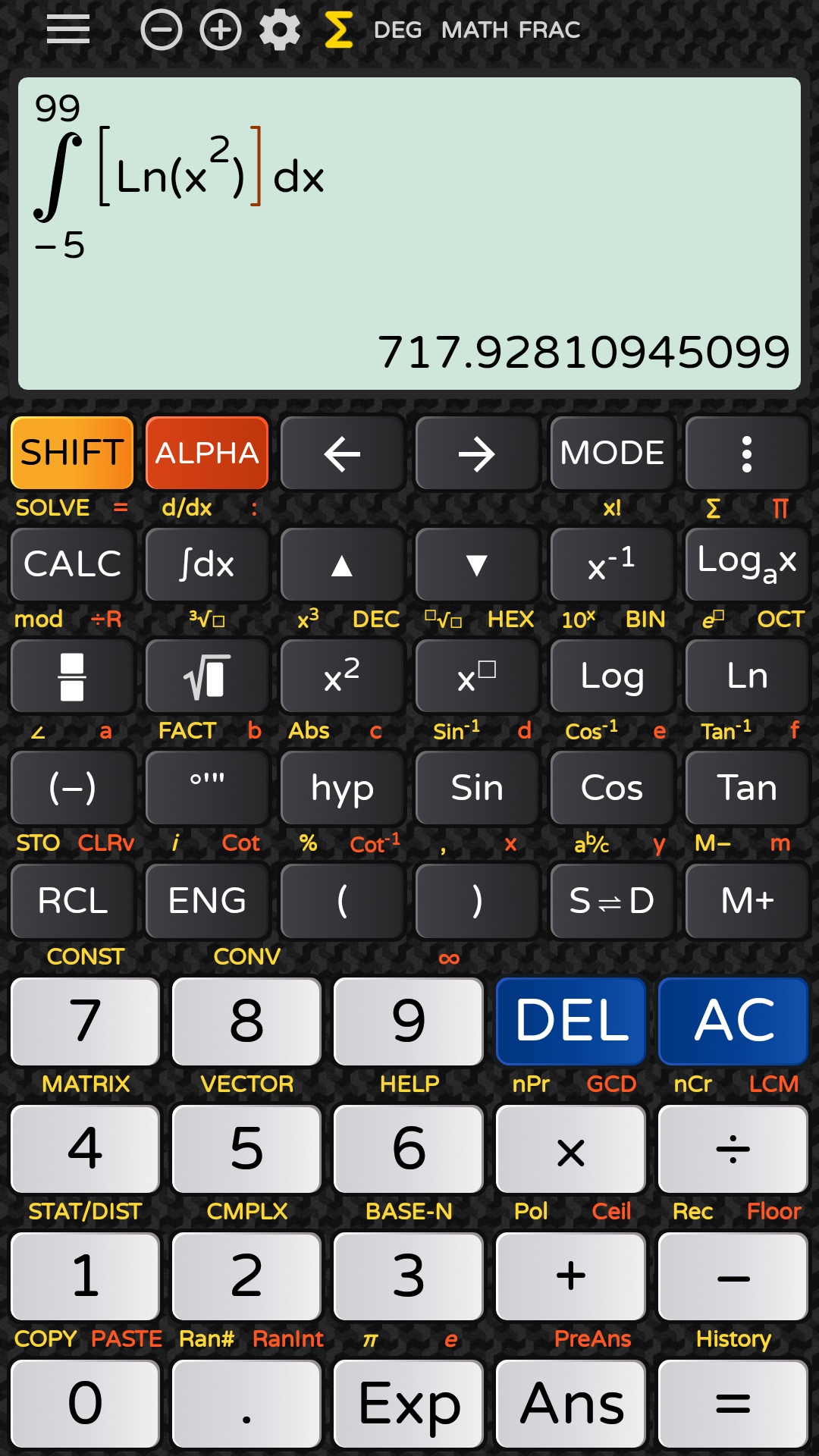
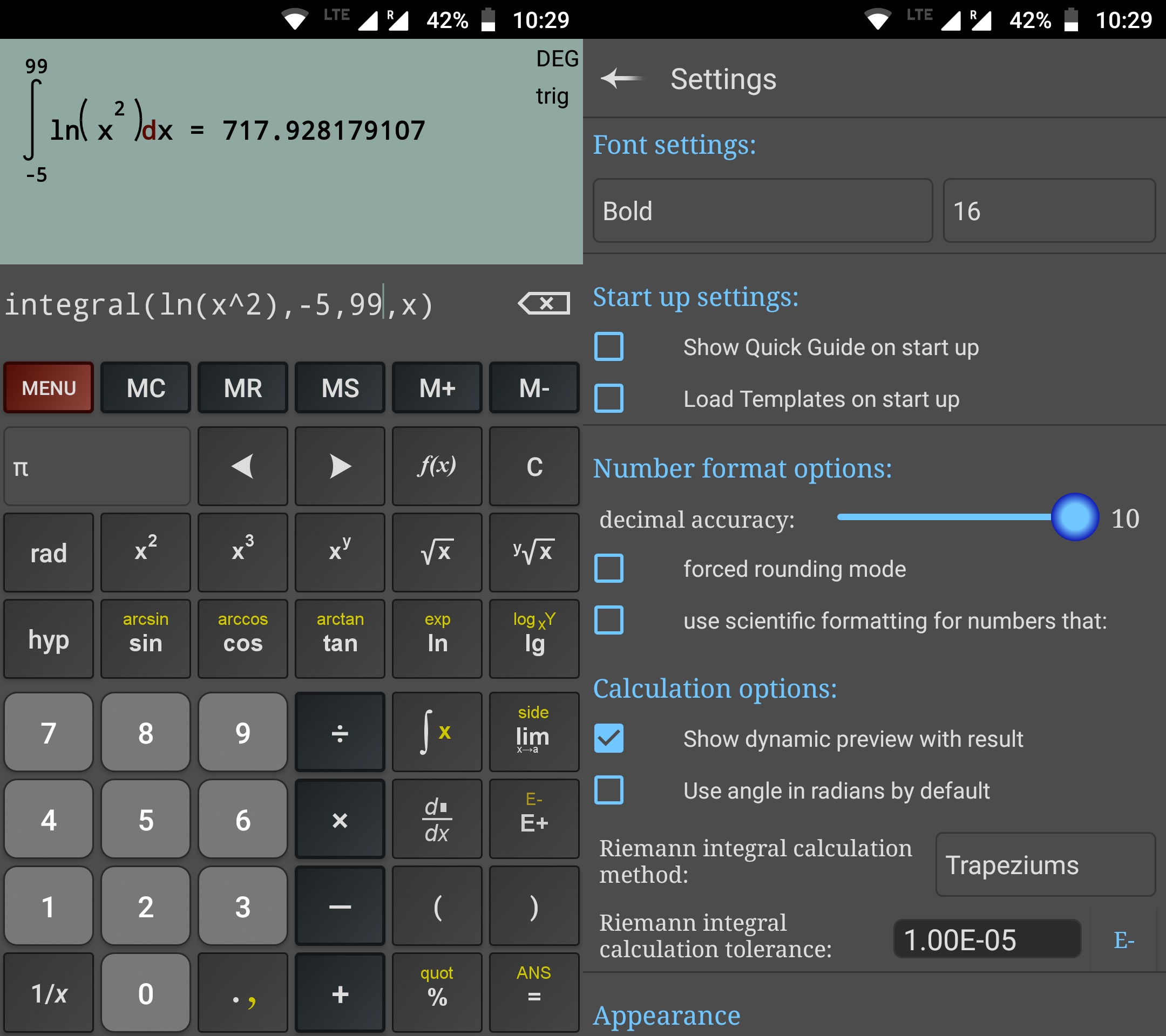
717.92810945 are indeed correct significant digits. So it’s crucial to be able to solve the integral first–but there aren’t many scientific calculators able to do that. Under Android, LisyThien’s four calc apps, Thien Studio’s five calc apps, GZ Group’s three calc apps and Mr Duy’s calc app (all 13 are identical, except for the default theming) are displaying 717.92810945099, which is fabulously accurate:
Let me now introduce you my everyday device, a cheap clone of something (we’ll talk later about clones and not-quite-clones of CASIO devices), the Olympia LCD-8310 that was sold by LIDL under the pseudo-brand UNITED OFFICE; it can’t solve, but it can calculate:

We don’t have the exact digits 717.92810945 on the screen, but 717.9281095 instead–the same value displayed by CASIO fx-991EX ClassWiz and fx-82DE PLUS both when solving the integral or calculating the logarithmic expression.
All the scientific calculators are internally using a better precision, they only display a rounded value. So by subtracting what we see on the screen (ANS- 717.9281095) we can find out what’s left inside: -0.000000049 in the case of my LCD-8310. Not convenient, let’s switch to ENG: -49.0082E^-09. Since it’s negative, we should have actually tried ANS- 717.9281094 and add this result to the original one; by doing so, we get the internal representation of the calculus: 717.9281094509918. The digits in bold are identical to Wolfram Alpha’s result, so we have 14 correct significant digits, although only 10 are displayed (of which the last one is rounded)!
How about the integral shown on the first physical calculator of this post, the German no-name but excellent GENIE 92 SC? Wolfram Alpha gives this:
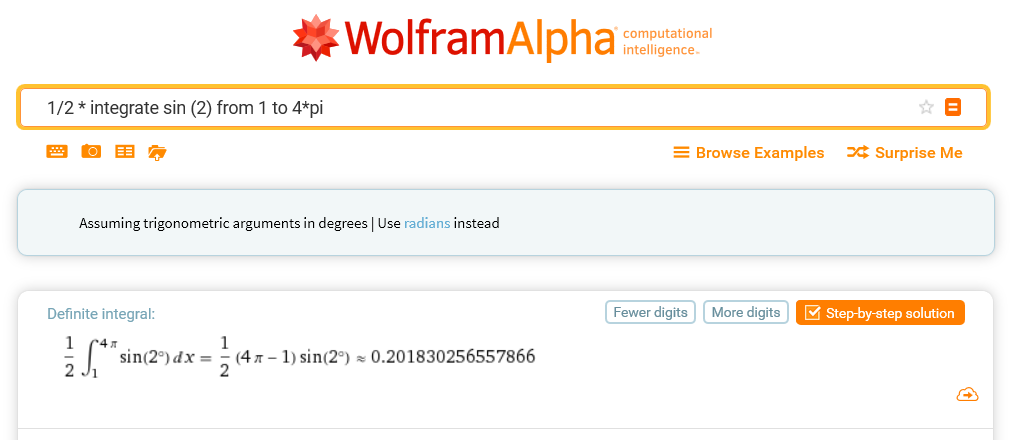
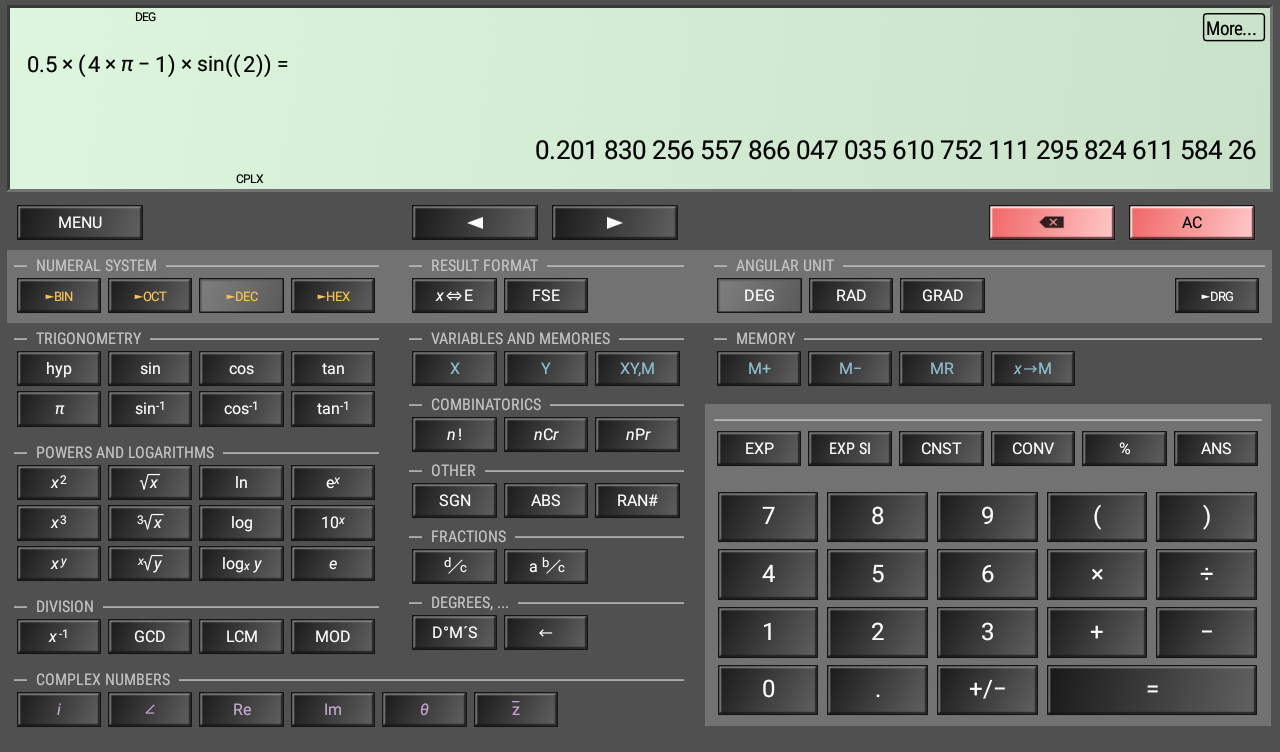
It’s a totally unimportant calculus, but for the sake of estimating the accuracy of a rather no-name device, let’s compare some displayed results for 0.5*(4*pi-1)*sin(2 in degrees), the digits identical to Wolfram’s in bold:
- GENIE 92 SC: 0.2018302566
- LCD-8310: 0.201830256 (0.2018302565578661 internally)
- Android’s stock calculator (8.1): 0.20183025655 (0.20183025655786604703 internally, so the last digit 5 should have been rounded to 6)
- CalcTastic: 0.201830256558 (0.2018302565578660470356108 internally)
- The 13 Vietnamese calculators, both as integral and as direct calculus: 0.20183025656 (0.20183025655786598564062 internally)
- The HiPER Scientific Calculator Pro: 0.20183025655786604703561075211129582461158426 (OMG!)
The last digit in WolframAlpha’s result isn’t necessarily correct, as it could have been rounded up (as it’s the case with any last displayed digit), but in this case it seems correct, as it’s followed by 0.
For once, Philip Stephens’ Scientific Calculator doesn’t display inaccurate results, but somehow it decides to show a different number of digits depending on what it’s told to calculate: the integral, or the direct formula:

Somehow, these errors are reminding me of the first calculator I’ve ever used, the original TI-30 (1976) with LED display (based on how fast it was depleting the 6F22/MN1604 battery, initially I thought it uses Nixie tubes). This bulky chap made history and it was extremely popular even in Europe (it cost about 30 DM at the time):

From memory, while it displayed Pi as 3.1515927, the internal representation was 3.1415926536. Otherwise, it was funnily inaccurate, but of the computational errors I discovered at the time only this one about e is mentioned online:
[1][INV][lnx] = 2.7182818 is displayed. Subtract 2.71 and multiply by 100: .82818301 is displayed; .82818284 are the correct digits. Why compute three extra digits that are not quite accurate?
No, it was to old to have been affected by this huge logarithm bug!
Either way, here’s a fact: the purely software calculators are usually more accurate than the hardware ones. For some reason, the chip designers went cheap on the methods and the tables used for floating point operations (anyone remembers the Pentium 5 FDIV bug?), and of course they couldn’t make use of any arbitrary-precision library.
This is why some people thought of a unified method of testing the accuracy of the handheld calculators. Enter Mike Sebastian’s Calculator Forensics page, now unfortunately outdated, and the most popular way of generating a calculator’s signature: the result of arcsin (arccos (arctan (tan (cos (sin (9) ) ) ) ) ). On modern devices or apps that use Postfix Algebraic notation (“Direct Algebraic Logic”), the formula is entered as above, on classical Prefix Algebraic ones it’s entered 9 sin cos tan arctan arccos arcsin. Note that 9 is meant to be in degrees, not in radians!
Some signatures for famous models:
- 8.99999863704 → Casio fx-82MS, fx-82TL, fx-115W, fx-115MS, fx-270W PLUS, fx-300MS, fx-300W, fx-570MS, fx-570W, fx-991MS
- 9.00001568547 → Casio fx-82 SOLAR, fx-82SX, fx-95, fx-991D, fx-991S, fx-991N, fx-580
- 9.0000157179 → Casio fx-900, fx-990, fx-991, fx-991M, fx-995, fx-961, fx-950
- 9.0000765511 → Casio fx-82D, fx-82L, fx-250C, fx-250D, fx-350M
- 9.177087103 → TI-30 (the original; did I mention how inaccurate it was?)
- 9.114640577 → TI-30 LCD, TI-30-II, TI-30-III
- 9.00000229461 → TI-30X, TI-30X Solar, TI-30Xa, TI-30Xa Solar
- 9.000003512065 → TI-30XIIB, TI-30XIIS
- 9.000001077372 → TI-30XS MultiView
- 8.99999863704 → TI-34
- 9.000003512065 → TI-34II
- 9.000417403 → HP-10C, HP-11C, HP-15C (maybe the most famous RPN calculators)
- 9.000000000 → HP-30S (“I believe this device uses true floating point for its transcendental calculations, instead of the traditional BCD (Binary Coded Decimal) of most calculators.”)
I suppose those were displayed values, not internal values. Since the results stopped being updated in 2002, there’s a lack of reports for the calculators that can be bought today. Let’s add some extra results then, starting with apps (I’ll list even devices I wasn’t able to test yet):
- Windows Calc, Android 8.1 Calculator, CalcTastic, HiPER Scientific Calculator, the 13 Vietnamese apps: 9
- Philip Stephens’ Scientific Calculator: 8.99999999983257
- Olympia LCD-8310, 229 functions, 2 lines: 8.999999998 (8.999999998078897 internally)
- STYLEX 38181, 240 functions, 2 lines, 10 €: 8.999999998 (8.999999998078897 internally)
- GENIE 56 SC, 228 functions, 2 lines, 9 €: 8.99999986 (same value internally)
- GENIE 82 SC, 240 functions, 2 lines, 13 €: 9.000000002 (9.000000002123857 internally)
- GENIE 92 SC, 580 functions, Natural Display, 18 €: n/a
- Casio fx-82MS 2nd ed., 240 functions, 12 lines, 12 €: n/a
- Casio fx-85MS 2nd ed., 240 functions, 12 lines, 24 €: n/a
- Casio fx-82DE Plus (fx-82ES Plus for Germany), 252 functions, 96×31 pixels Natural-V.P.A.M., 20…23 €: 9.000000007 (9.00000000733338 internally)
- Casio fx-85DE Plus (fx-85GT Plus for Germany), 252 functions, 96×31 pixels Natural-V.P.A.M., 26…28 €: n/a
- Casio fx-991ES, 403 functions, Natural Display: n/a
- Casio fx-991ES Plus, 417 functions, Natural Display: n/a
- Casio fx-87DE Plus, 502 or 510 functions, Natural-V.P.A.M., 28…30 €: 9.000000007 (9.00000000733338 internally)
- Casio fx-87DE X (dumber edition of fx-991DE X, no matrix, vector and complex numbers) ClassWiz, 192×63 pixels Natural-V.P.A.M., 593 functions, 30…33 €: 9.000000007 (9.00000000733338 internally)
- Casio fx-991DE X (fx-991EX for Germany) ClassWiz, 192×63 pixels Natural-V.P.A.M., 696 functions, 32…40 €: 9.000000007 (9.00000000733338 internally)
- HP-10s+ (NW276AA), 240 functions, 2 lines, 10 € MSRP: 9.000000002 (9.000000002123857 internally)
- HP 300s+ (NW277AA), 315 functions, 96×31 pixels Natural Display, 16 € MSRP: 9.000000001 (9.000000000881497 internally)
- Casio fx-82SOLAR II, 144 functions, 1 line, 17 €: 9.000007164 (9.0000071639 internally)
- Sharp EL-501X, 130 functions, 1 line: 8.999998637
- Sharp EL-506X, 469 functions, 2 lines: n/a
- Sharp EL-W506X WriteView, 556 functions, 96×32 pixels Natural Display: 9.000000099 (9.000000098906 internally)
- Sharp EL-W550XG WriteView, 335 functions, 96×32 pixels Natural Display, 20 €: 9.000000099 (9.000000098906 internally)
- TI-30 ECO RS, 1 line: n/a
- TI-30X IIS, 2 lines: n/a
- TI-30X Plus MathPrint, 4 lines, 192×64 pixels MathPrint/Classic, 29 €: 8.99999986 (8.999999860032 internally)
- TI-30X Pro MathPrint, 4 lines, 192×64 pixels MathPrint/Classic , 35 €: 8.99999986 (8.999999860032 internally)
- TI-36X Pro, 4 lines, 96×31 pixels MultiView: n/a
Note that from the above physical calculators, only Casio fx-991EX (and DE X) ClassWiz and TI-36X Pro are able to perform both Differentiation and Integration and Matrix Calculus; that Differentiation and Integration can also be solved by GENIE 92 SC, Sharp EL-W506X WriteView, Casio fx-991ES (and Plus); that not a single of them is programmable or graphing; but that almost all 2-line models are capable of statistics (Standard Deviation, Quadratic Regression).
Despite the fact that a result starting with 9.000… is aesthetically more pleasant than one starting with 8.999…, displayed values of 8.999999998 and 9.000000002 both mean the error is 2e-9. Sorting the devices by the approximate errors (absolute values), we notice that some of the devices that start with 9.0 are actually less precise than the others:
- 0.7e-9: Casio fx-82DE Plus, fx-87DE Plus, fx-87DE X, fx-991DE X (likely true for non-DE editions too)
- 1e-9: HP 300s+
- 2e-9: Olympia/United Office LCD-8310, Stylex 38181, GENIE 82 SC, HP-10s+
- 99e-9: Sharp EL-W550XG
- 140e-9: GENIE 56 SC, TI-30X Plus MathPrint
- 1363e-9: Sharp EL-501X
- 7164e-9: Casio fx-82SOLAR II
So far, the worse of all is Casio fx-82SOLAR II, but once I try the TI-30 ECO RS, things might change. Either way, Texas Instruments remains one of the worst choices ever.


Knowing all this, why would anyone use a physical calculator instead of an app or, when sufficient, of the Windows Calculator, and then of something like Excel for what it’s worth? Of course, I don’t know how to work with integrals, differentials, matrices, system of equations and other advanced tasks in Excel or any Windows program, but this is another issue; for now I’m not very familiar with the apps that can do that in Android either–specifically these four calc apps and these other five calc apps. Besides, the most potent smartphone calculator apps are not made by the likes of Casio, but by Mister Nobody of Somewhere, so how can anyone tell anything about the potentially quirky bugs?
To me, the inaccuracies in handheld calculators remind me of the mechanical watches: definitely less accurate than the quartz-powered ones (even the thermally uncompensated quartz is nowadays very satisfactory), and yet some people are huge fans of them. Moreover, there are people who “collect” several “dress watches” (even quartz ones), “weekenders” or sport watches, just so they can wear one or another depending on their mood and apparel. Is there anyone doing the same with pocket or handheld calculators?
What actually makes such devices sell can be resumed in two words: kids and schools. In all of the developed countries there are calculators that have been “certified” and authorized to be used in class and in exams, but what’s worse is that some such devices are strongly recommended or even required, so what can parents do other than purchasing them? It’s less relevant that in my time kids didn’t need any calculator to learn how to simplify fractions or how to perform some other elementary tasks for which nothing is needed but an IQ over 80. Casio, Texas Instruments, Sharp and others must sell their devices, so they lobbied the powers that be. For the sake of the public education, right?
Aaaaand… there are huge differences between countries. You’ve already noticed that Casio has special editions for Germany, with the firmware in German and with a comma instead of the decimal point. Other countries are having their idiosyncrasies too (there are Latin American, Spanish and Central European editions of fx-991EX, with a different number of functions: 553 for LA X, 575 for SP X, 668 for CE X, vs. 696 for DE X and 552 in the international EX; most extra functions for CE and DE are unit conversions), but let’s take France for now.
Here’s the fx-92+ Spéciale Collège, a device found nowhere on Planet Earth but in France. Being “adapted” to collège (the first 5 years of the secondary education), not lycée (the last 3 years of the secondary school), it doesn’t feature any differential and integral calculus capabilities, but it has rudimentary programming features (plutôt bidon si vous voulez mon avis). But I like the color of the case 🙂

Otherwise, the French version of the color graphing calculator fx-CG50 is called Graph 90+E and since Sept. 2018 it can run Python! But it costs 80 € chez Darty (130 € MSRP when launched). The good news: although specifically made for the requirements of the French educational system, the OS update 3.2 with Python can also be installed in fx-CG50.
The other major player, TI, also aims high: TI-83 Premium CE is soon to benefit of a Python interpreter, unfortunately via an external adapter. But even without Python, Texas Instruments offers online support for various educational activities involving his advanced calculators. Incidentally, this made me learn of the Paradox of the Grand Duke of Tuscany–something I couldn’t find in Wikipedia!
From their materials I’ve learned that Galileo Galilei, while in Florence at the Court of the Duke of Tuscany, wrote up a paper in 1620 to explain a situation that the Duke himself noticed during the parlor games popular at the Court. The Duke had noticed that rolling the dice three times and summing the values led to the sum 10 slightly more often than the sum 9, despite the fact that both sums can be obtained in 6 ways:
10 = 6+3+1 = 6+2+2 = 5+4+1 = 5+3+2 = 4+4+2 = 4+3+3 9 = 6+2+1 = 5+3+1 = 5+2+2 = 4+4+1 = 4+3+2 = 3+3+3
The students are supposed to use a TI calculator in order to reproduce the situation and explain it. The explanation? Of the 6x6x6 = 216 dice values possible in 3 runs, only 25 lead to the sum 10, while 27 lead to the sum 9:
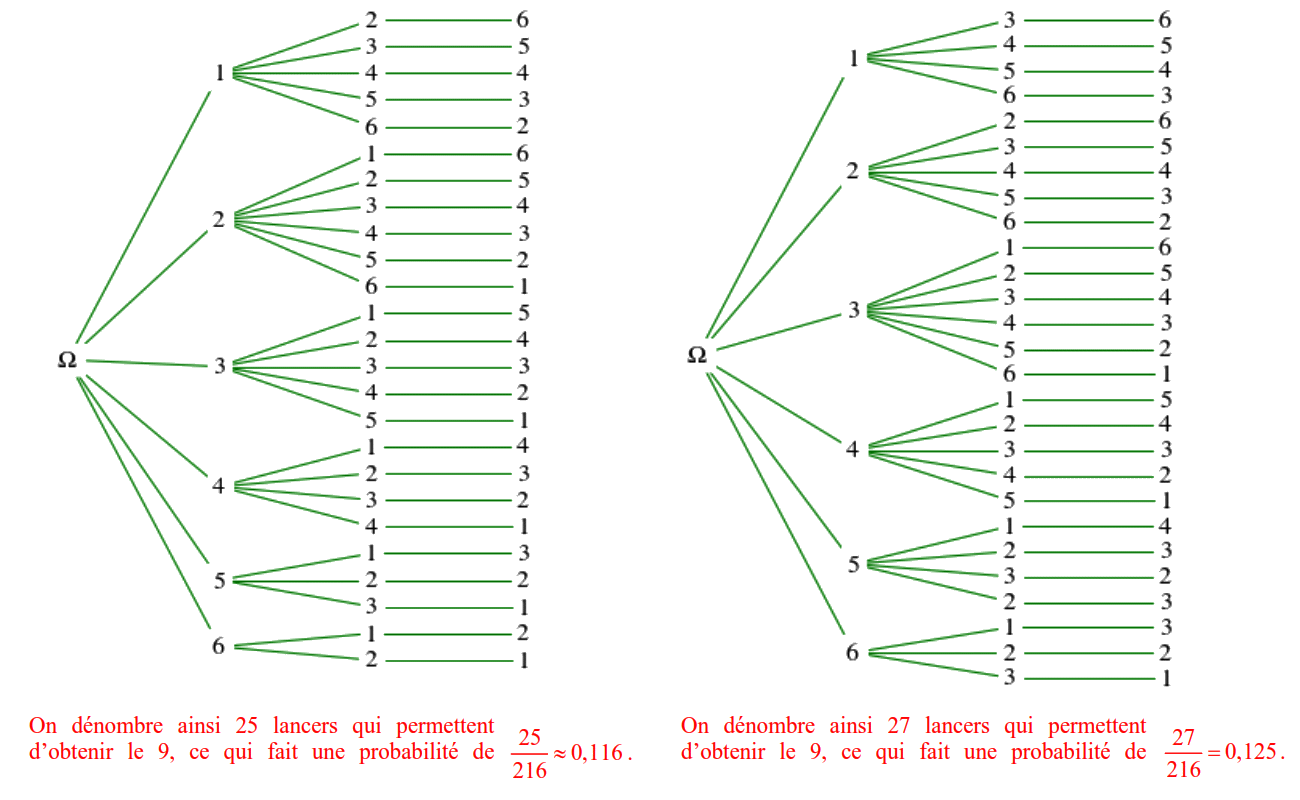
Nice, but no need for an expensive calculator to solve this problem!
Something about the two HP calculators mentioned above–the HP 10s+ and HP 300+, the only two models of relevance that HP sells nowadays. Their main quality: they’re elegant.

The thing is, these are marketing images, not real photos. You’ll find anywhere (at least on Amazon.com and Amazon.it) people complaining that the screen has an abysmal contrast, that everything is reflective and it’s hard to see everything regardless of the level of the ambient light and–most important maybe–that the buttons are simply crappy:
Reports of missed key presses with this calculator are NOT exaggerated. This one is an exam grade killer! … The features are great for the price but it must be watched very closely or your results will be incorrect.
I can’t believe HP actually put their name on this device. I have HP Voyager calculators purchased in the early 1980s which still work flawlessly as they did when new. No missed key presses with them. Evidently HP no longer builds any level of quality in their non-graphing calculators. If Amazon allowed less than one star, this item deserves it. Returning this thing today.It is very important for your calculator to accept the inputs from buttons 100% of the time, expecially under a time crunch or during an exam. This fails to do just that, where random times, may 75% of button presses actually register, I do believe it has something to do with the way the buttons are made, where the edges of the buttons don’t cause the input detection, but a small dot in the center of the buttons do, so if you’re always very careful, sure maybe it isn’t so bad, but I expect better from HP.
Truth be told, nobody makes hardware the way they used to in the 70s and the 80s. CASIO has the best quality of all, and Sharp is not that bad either (I can’t tell of Canon), but HP is horrendous. Even as they re-released a special edition of the legendary HP 12C Financial Programmable Calculator back in 2012, people started complaining about the total garbage that HP calls buttons. Absolutely anything to do with the old HP dependability and quality. Cheap crap that even the worst fake Chinese clones (think CTTTZEN calculators) don’t have.
This being said, in a world where 90% of the scientific calculators seem to be a clone of some variant of Casio fx-82MS, are HP’s 10s+ and 300s+ really using some chip designed by or for HP, or are they yet another set of clones? The first answer you’ll find: «They are so much of a clone that the menus themselves read CASIO» (with instructions on how to get CASIO on the screen).
Well, not so fast. Remember the “forensic test” that should get back 9 after some trigonometrical functions? In a thread on HPMuseum.org, someone got for HP 10s+ the result 9.000000002123857 (that’s the internal representation), and «None of the CASIO models listed have this HP signature result.» The same for HP 300s+ (9.000000001 on screeen, 9.000000000881497 internally)–«Again, no CASIO models listed have this signature.»
The explanation: «both HP and CASIO shared a common software base developed by Kinpo TW in China and compiled to run on distinct hardware platforms. This would explains why both have the same menu structures and many common functions.»
Of course, this doesn’t fix the poor screen and crappy HP buttons. Simply put, CASIO is the king, and fx-991EX, whatever you call it, is the mother of all calculators, both in build quality and features:

And it also can do that (the left picture):

Not everything CASIO is that shiny though. fx-82SOLAR II is nicely packaged garbage, and I wasn’t able to test the “2nd editions” in modern but bland casings:

Speaking of editions, TI had the bad idea not only of calling too many models “TI-30 something” but also to use the VW approach: let’s just call them Golf, Polo and Passat, no matter they change in time! Here’s 3 editions of the same TI-30X IIS–which one would you receive when ordering online?

The basic calculator has one more quirk: the solar-only TI-30 ECO RS, supposedly just an “eco” edition of TI-30Xa (the contemporary entry-level TI-30), has a specific design in Germany–guess which one?

The fucking picture in the middle is the German edition! Potthässlich. And it still has a decimal dot, not a comma, as it’s not a Casio!
This company has some of the worst designers–people who have never read The Design of Everyday Things. Sure thing, not all their products are as ugly as TI-36X Pro, but their attempt of a HP-like elegance somehow failed in my opinion:

The only good thing is that the keys are toggling between values: instead of using SHIFT and ALPHA, by repeatedly pressing SIN one would get sin, arcsin, sinh. And yet, these bulky objects are uninspiring… and not that rich in features (which is consistent with the TI-30 tradition, huh).
I’m going to end with a video. Remember the «integrate ln (x^2) from -5 to 99» test in which an Android app failed lamentably? Someone compared the speed of three devices performing nothing else but this calculus! Casio fx-991EX Classwiz vs Canon F-789SGA vs Casio fx-991ES:
- fx-991EX Classwiz: about 45 seconds (35 seconds, claim 2 comments)
- fx-991ES: some 3 minutes 12 seconds
- Canon F-789SGA: about 4 minutes 40 seconds
From the comments:
- fx-991ES Plus: 2 minutes 54 seconds
- HP 35s: 52 seconds
- TI-83 Plus: 26 seconds
- Sharp EL-W506X: 17 seconds (finally, a fast chip!)
- Sharp EL-W516X: 15 seconds (unfortunately, discontinued model)
Well, I’m impressed by Sharp’s speed (is the lower precision the price to pay for an Autobahn-like speed?). EL-W506X’s speed and keyboard precision is praised by users here and here. Quite a surprise for an under-25 € device. The HP and TI devices are in a higher price class, and HP 35s has such an impressive list of bugs that makes TI look good. As for all these devices that seem to be running at 4.77 MHz… they might be running at an even lower speed: «The 35s is using 1980’s technology–its 8502 processor core primarily.» And, to no one’s surprise, the keys are not always registering and they’re failing after 2, 10, 12 months…
For the time being, I’m going to play with some Android apps though.
UPDATE 1: Following a comment on Hacker News, which pointed to These two Casio calculators showing different answers for same input, I just got a new aspect to consider:

Which calculators (generally speaking, not just with regards to the two shown devices) are using the correct priority of operations? And which is the “correct” one?
The explanation for the above situation can be found in the user’s guide for each device:

The first device, fx-991ES, uses the correct order of the operations (which, BTW, is PEMDAS), performing a strict left-to-right interpretation of the explicit and implicit multiplication and division operators. The second one, fx-991ES PLUS, chose by design to give a higher priority to the implied multiplication (“multiplication where the multiplication sign is omitted”). I can understand that some people might consider that omitting the multiplication sign somewhat “creates a tighter bond” between the operands, but there is no rule to state that. I can only think of CASIO as of a company that gave way to the idiots when designing newer devices.
UPDATE 2: Someone thinks I don’t understand how such calculators work (of course I don’t, as I have never designed one); and that Casio calculators “are actually just computing the integrals numerically and then converting to fractions because the error in result was smaller than the the threshold needed to convert it to a fraction.” (I suppose computing means using some Newton-Cotes rule, the most common being trapezoidal and Simpson’s. I suppose I was expecting too much.)
Note that the fact that some devices default to fraction mode doesn’t change the fact that they can also display e.g. 0.5 instead of 1/2. And fractions are only displayed as a result when the input was fractional; if I enter “0.33+0.17” the device should not display 1/2, but 0.5 (I have not checked yet, but if they think otherwise at Casio, they’re insane).
Threshold or not, why can’t they display 9 instead of 9.000000007? What is that threshold if 0.7e-9 not small enough? This means that computing integral(sin(x)dx from 0 to pi/3) is done with better precision than 0.7e-9.
A theory that makes sense: Casio is officially using 15 digits for internal representation (note that TI only uses 13 digits internally, and pi is used with 12 digits!); it normally shows 10 digits to the user, but with epsilons it seems confident about showing values of 1e-13 (why not 1e-12?!). And a sequence of trigonometric operations is lossier than a simple integral (at least with Casio; possibly not with TI).
UPDATE 3: When I watched that video and I said I was impressed by the speed of Sharp EL-W506X, I added: “is the lower precision the price to pay for an Autobahn-like speed?”. This forum thread reveals how this device trades accuracy for speed:
- integral(sin(x)dx from 0 to pi) = 2.000000001, “and it took 23 seconds to compute this. Consulting the user guide I found the reason for the above odd result. We need to specify a higher number of sub-intervals, as by default this calculator will use just 100 intervals. Trying again but specifying 200 intervals, we got the usual expected result of 2. To get this answer the machine took 44.5 seconds.”
- diff(3x^3), x=1 = 9.00000001. “Checking the user guide, we see that for this computation the machine uses a default minute interval of 10^-5. Trying again but specifying a minute interval of 10^-8 it came out with the usual expected answer.”
- “Trying a fx-991, the above integral and differential gives the expected results of 2 and 9 without the need to specify additional command options. The ClassWiz took just under 2 seconds to compute the integral.”
So I suppose CASIO likes being a winner. (Not that they didn’t have bugs; have fun crashing fx-115MS, and learn about its asinh bug similar to TI’s logarithm bug.)
UPDATE 4: As I am playing with the aforementioned 13 Vietnamese apps, I’m annoyed by this deceitful practice of releasing duplicates of the exact same app with: different names; different icons; different developer name; different default theme (once you pay, the Pro mode allows selecting any of the 32 themes present in each of the 12 apps); ugly icons; stupid names (horrendously random and unsystematic; and pretending to emulate a random scientific calculator). Here’s a list of them:
- com.calculator.tool.fx350ex – “Calculator 82 350 570 991 ex es ms vn plus fx”
- com.duy.calc.casio.v2 – “School scientific calculator 500 es plus 500 ms”
- com.duy.calc.graph – “Graphing calculator ti 84 – simulate for es-991 fx”
- com.duy.tool.calc.colorful – “Fx Calculator 350es 84+ calculator sin cos tan”
- com.duy.tool.calc.fx580.v2 – “Calculator 570 ex 991 ex – Fraction calculator fx”
- com.mrduy.calc.ti36 – “Complex calculator & Solve for x ti-36 ti-84 Plus”
- com.nstudio.calc.casio.business – “Advanced fx calculator 991 es plus & 991 ms plus”
- com.nstudio.calc.casio.modern – “Free engineering fx calculator 991 es plus & 92”
- com.nstudio.calc.casio.office – “Algebra scientific calculator 991 ms plus 100 ms”
- com.nstudio.calc.casio.retro – “Natural mathematics display fx calculator 991 ms”
- com.nstudio.calc.casio.tavern – “hp 35s fx Scientific Calculator 570 es plus free”
- com.tool.calculator.casio.fx991.es.plus – “Math Camera fx calculator 991 es emulator 991 ex”
- com.tool.calculator.casio.programmable – “X84 Fraction calculator Programmable 991 ex es fx”
This marketing technique is usually employed by fraudulent apps, but these seem not only legit, but excellent. Still, who the heck has the time to investigate their potential errors? Even reading the comments in 12 different places is… arghh. Speaking of bugs, as I am writing this, the developer wasn’t able to sync all his apps:
- 1 app is in version 3.8.5-03-01-2019-12-release, with 1.99 € IAP
- 5 apps are in version 3.8.5-07-01-2019-21-release, with 1.99 € IAP
- 5 apps are in version 3.8.6-15-01-2019-17-release, with 1.99 € IAP
- 1 app is in version 3.8.6-15-01-2019-17-release, with 2.09 € IAP
- 1 app is in version 3.8.7-27-01-2019-02-release, with 2.09 € IAP
I wouldn’t even contemplate using such an app if there were better apps in Google’s Play Store.
March 4 EDIT: all apps but one have been updated to 3.9.1-03-03-2019-13-release. The IAP values are still different.
UPDATE 5: To dismiss Canon as a potential worthy competitor, here’s some results from a Speed Test: Casio fx-991EX Classwiz vs Canon F-792SGA.
- integral (sin(x)/x dx from .001 to 0.06)
- fx-991EX Classwiz: 1.75 s
- Canon F-792SGA: 6 s
- integral (e^-x dx from 0 to 100)
- fx-991EX Classwiz: 2.75 s
- Canon F-792SGA: 19 s
- Solve e^x + .2x^3 = 3
- fx-991EX Classwiz: 1.75 s
- Canon F-792SGA: 12.7 s
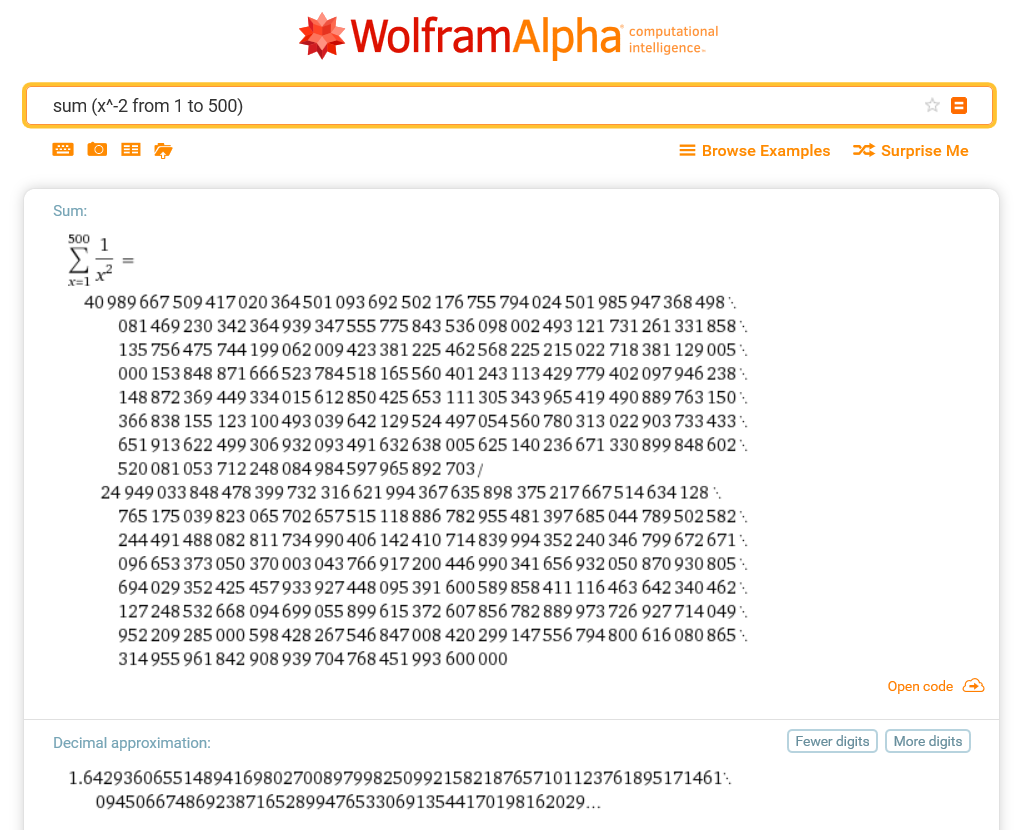
- sum (x^-2 from 1 to 500)
- fx-991EX Classwiz: 23 s
- Canon F-792SGA: 2 min 18 s
Canon seems up to roughly 7 times slower. Either way, no calculator can give an answer like WolframAlpha’s:
UPDATE 6: As I was playing with some Android calculator apps, I was struck by the memory of what I would have wanted a calculator to have back in 1982-1983: Least Common Multiple (LCM), Greatest Common Divisor (GCD) aka Highest Common Factor (HCF), Prime Factorization. The strange thing is that even today, most calculators don’t have such elementary capabilities!
When the do have them, LCM and GCD are secondary functions to the multiplication and division buttons:

Casio doesn’t factorize for prime numbers of more than 3 digits:

Now the amazing thing is how the presence or absence of this 6th-grade arithmetic is spread among Casio’s models:
- Having GCD, LCM: fx-115ES, fx-991ES, fx-87DE Plus, fx-87DE X, fx-991DE X.
- Not having GCD, LCM: fx-82MS 2nd Ed., fx-82SX Plus, fx-82EX, fx-82ES Plus, fx-82DE Plus, fx-85EX, fx-85ES Plus, fx-85GT Plus (fx-85DE Plus), fx-220 Plus 2nd Ed., fx-350EX, fx-350ES Plus, fx-570ES Plus, fx-991ES Plus (the non-Plus had it!), fx-991EX, fx-3650P II (programmable).
The most outrageous part is that the international fx-991EX ClassWiz (left) lacks GCD and LCM, whereas the German edition fx-991DE X (right) has them!

WTF, Casio?!
But things can get equally illogical at Sharp. With them, one has to chose between 6th-grade arithmetic (GCD, LCM and quotient/remainder) and 10th-grade calculus (derivatives and integrals, matrix calculus, etc.)–there’s no current calculator to feature both sets of features, no matter how many hundreds of functions they claim to have!
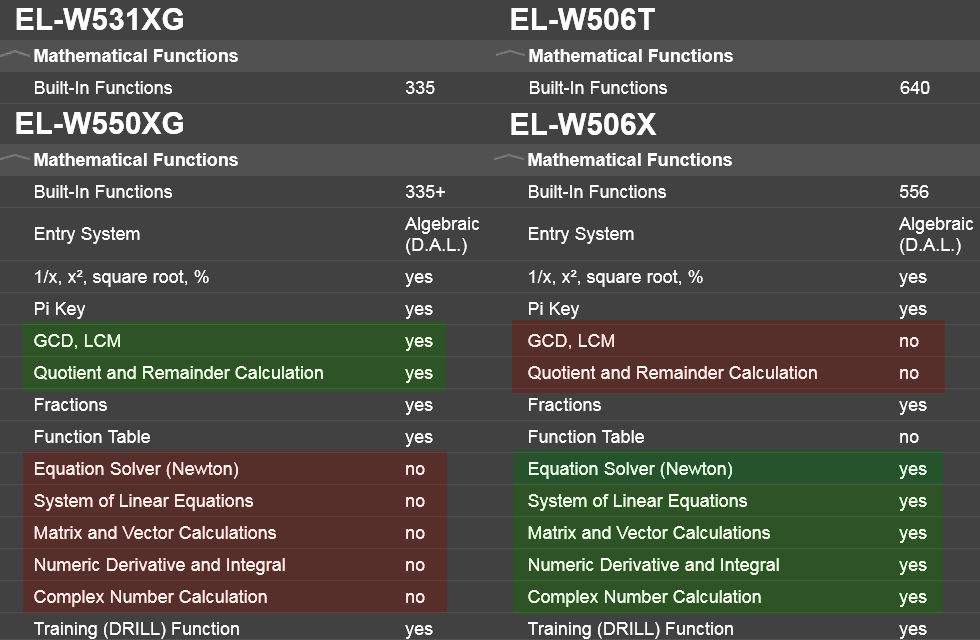
At least we can find some logic with Texas Instruments: whenever such a calculator has a “math” button (e.g. TI-30X Plus/Pro MathPrint, TI-30X Pro MultiView, TI-36X Pro), you’ll find GCD, LCM and factorization among the functions hidden under that button! (It’s just they’re not printed anywhere around the button.) But TI-30XS MultiView lacks such a button.
UPDATE 7: Revelations on TI, courtesy of the regional government of Baden-Württemberg and of the Datamath Calculator Museum! Did you know the differences between these two series of calculators, and between each series’ Plus and Pro models?
- TI-30X Plus MultiView and TI-30X Pro MultiView (cased like TI-36X Pro)
- TI-30X Plus MathPrint and TI-30X Pro MathPrint (rectangular case with rounded corners)
The Plus models are a dumbed-down versions of Pro that lack the support for the following features that are not accepted in high-school exams in Bavaria and Baden-Württemberg: numeric derivative, numeric integral, numeric equation solver, polynomial solver. (This explains why TI-30X Plus MathPrint is much easier available in Germany than the Pro edition: most people are purchasing the device authorized in exams!) You have to understand that the Plus models are featuring the exact same chip as the Pro, but some features have been blocked. However…
It is rather unusual to discontinue and replace a scientific calculator within just three years after its introduction but in this case there was a serious reason behind the unexpected move from Texas Instruments. In July 2017 the Ministry of Education, Youth and Sport of Baden Württemberg, Germany informed all schools in the State that it is known since March 2017 to “hack” with a few keystrokes the TI-30X Plus MultiView and upgrade it to the original TI-30X Pro MultiView.
So, after having initially announced an updated OS for the TI-30X Plus MultiView (to disable the hack), they finally decided to release a new line:
Texas Instruments announced on February 20, 2018 at the didacta 2018, an Education Trade Show in Germany, with the TI-30X Plus MathPrint and TI-30X Pro MathPrint the stylish successors of both the TI-30X Plus MultiView and TI-30X Pro MultiView.
The TI-30X Plus MultiView was already dead, because it wouldn’t have make sense to sell for less a calculator that could have been upgraded for free to its more expensive version! And it was banned in exams anyway…
So this is what’s left on the German market; it’s easy to see what’s missing as the 2nd function of the buttons in the Plus:

The most advanced calculators authorized in Abitur (≈A-level, ≈baccalaureate) exams in Southern Germany: TI-30X Plus MathPrint, Casio fx-87DE X ClassWiz, Casio FX-87DE Plus, Sharp EL-W550XG WriteView.

And now, the very last test: remember the speed comparison at UPDATE 5? I’ve tried sum (x^-2 from 1 to 500) on a TI-30X Plus (the integrals & solver are only available in Pro): it took exactly 23 seconds (or rather about 22.5 s), the same as Casio fx-991EX!

UPDATE 8: Still looking for a decent Android app able to perform advanced calculus tasks (e.g. integrals) that CalcTastic wouldn’t do, and that Philip Stephens’ calculator can do with unacceptable errors. The dozens or so of Vietnamese clones of each other are pissing me off.
It seems an impossible task. Here’s Direct Scientific Calculator by Noskovtools Software: editing an expression is hideously painful, and the integral error is slightly higher than that of a TI-30X Pro/TI-36X Pro, in all cases using the default ε=1e-5:
The error is even larger in J.J. Software’s Full Scientific Calculator, which is tremendously slow to integrate (but otherwise fine for solving elementary equation systems for lazy kids):
Recap:
- Correct digits: 717.92810945099
- The Vietnamese apps: 717.92810945099
- Casio fx-991EX: 717.9281095
- TI-30X Pro/TI-36X Pro (ε=1e-5): 717.9281268
- Philip Stephens: 717.9690502
- Direct Calculator (ε=1e-5): 717.928179107
- J.J. Software: 717.912154
Everyone makes apps, and all such apps suck. Sigh.
UPDATE 9–revisiting the 13 Vietnamese apps (see UPDATE 4): notwithstanding the difference in the IAP (€1.99 or €2.09), at the beginning of March only one of them was at version 3.8.7, six at 3.8.6 and six at 3.8.5, but… but there are newer beta versions available! Only 5 apps offered me the opportunity to join the beta program, but I know that other people could also join some of the other ones. From those available to me, four had 3.8.9-beta-26-02-2019-03-release, and the fifth had 3.9.0-28-02-2019-23-release (no beta in name!).
The improvements and bug fixes seem to be minor, as the bug reported for one of the apps by a certain A.L. Wright (to which the developer dumbly replied: “Thanks for your review. We will improve this app more and more. If you have a problem, you can send your feedback to Email: tranleduy1233@gmail.com”) is still there even in 3.9.0: such approximations of e cannot be calculated, as the app enters an infinite loop:
Even the stock calculator can do it:
I then ran into an unexpected error while trying a sum that even Philip Stephens’ app managed to compute with surprisingly good accuracy:
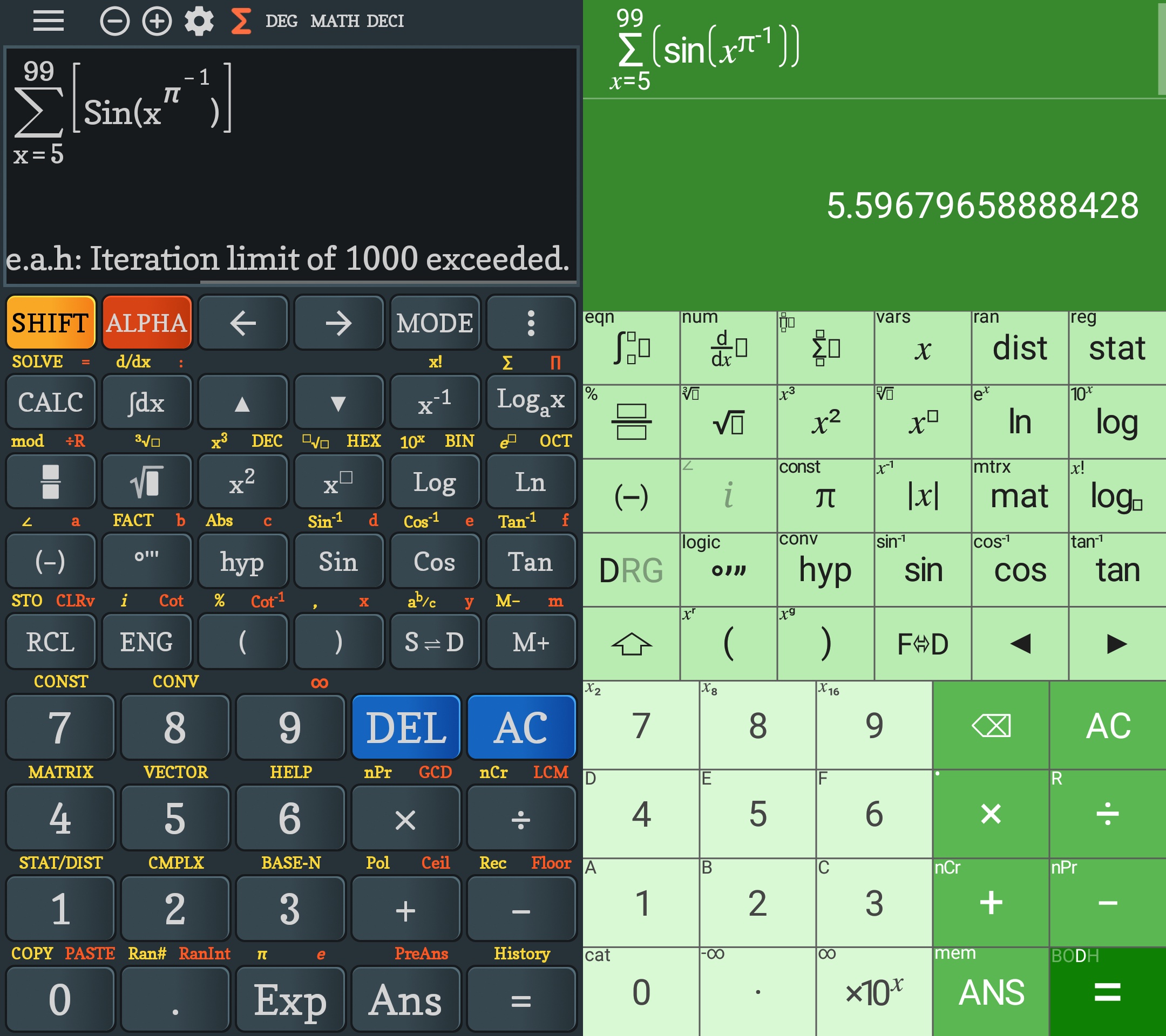
Wolfram Alpha approximates the result to 5.596796588884281230… (therefore all the digits above are exact!), but for the Vietnamese apps it’s…
Math Error: org.e.c.e.a.h: Iteration limit of 1000 exceeded.
EDIT: OK, now at 3.9.1-03-03-2019-13-release, and the bugs are still there.
UPDATE 10–playing with more apps! When I first tried HiPER Scientific Calculator Pro, it didn’t have integral calculus capabilities, but all of a sudden I noticed that in version 6.4.1 a button has changed to add integrals and derivatives!
Unfortunately, there’s something terribly wrong with this app. In complex mode, it solves the integral that should give 717.928… to a complex number, and in real mode it errors out!
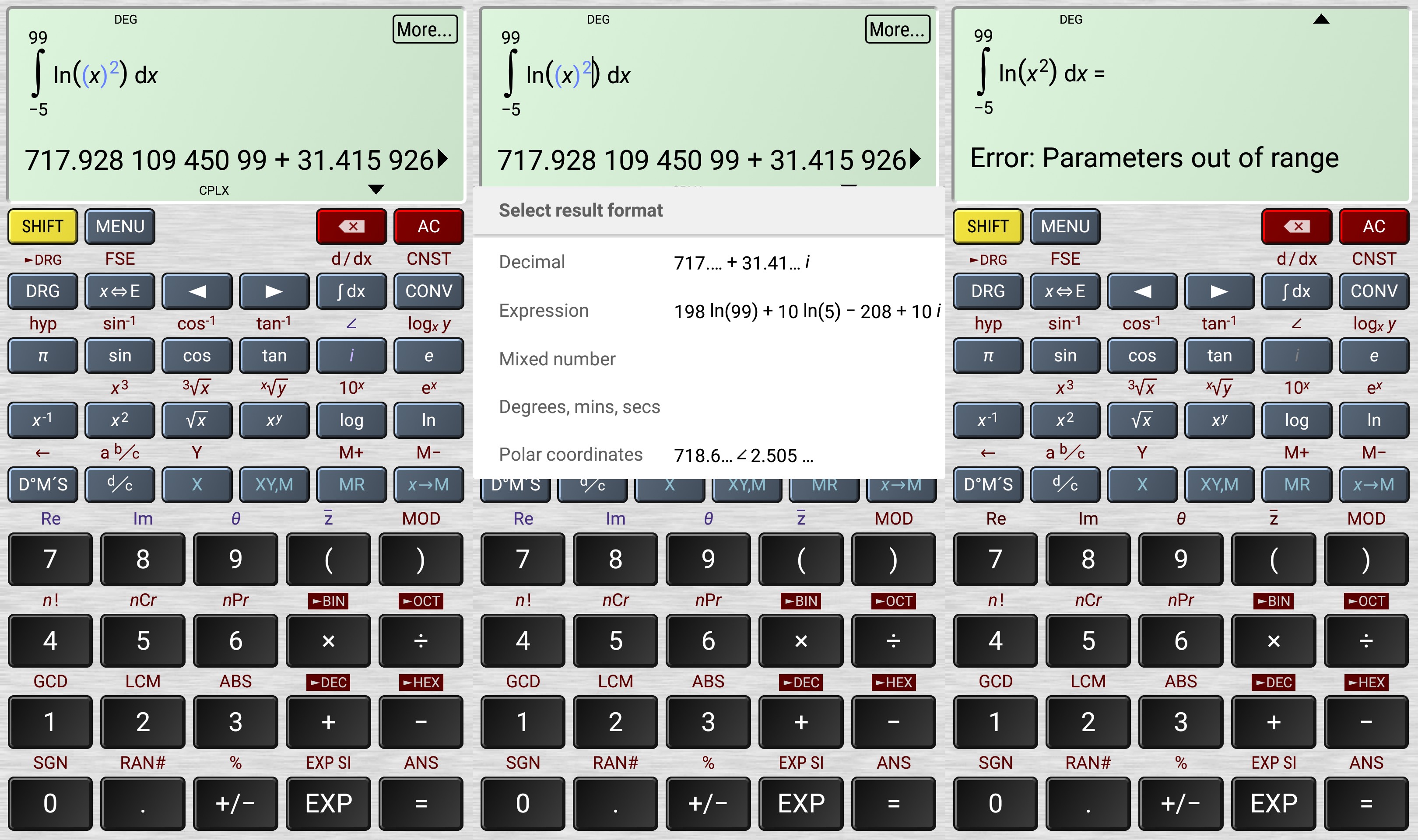
So right now, you’d better not waste your time money with this app. It also fails with the integral from 0 to 99, which should give 711.833730326649…
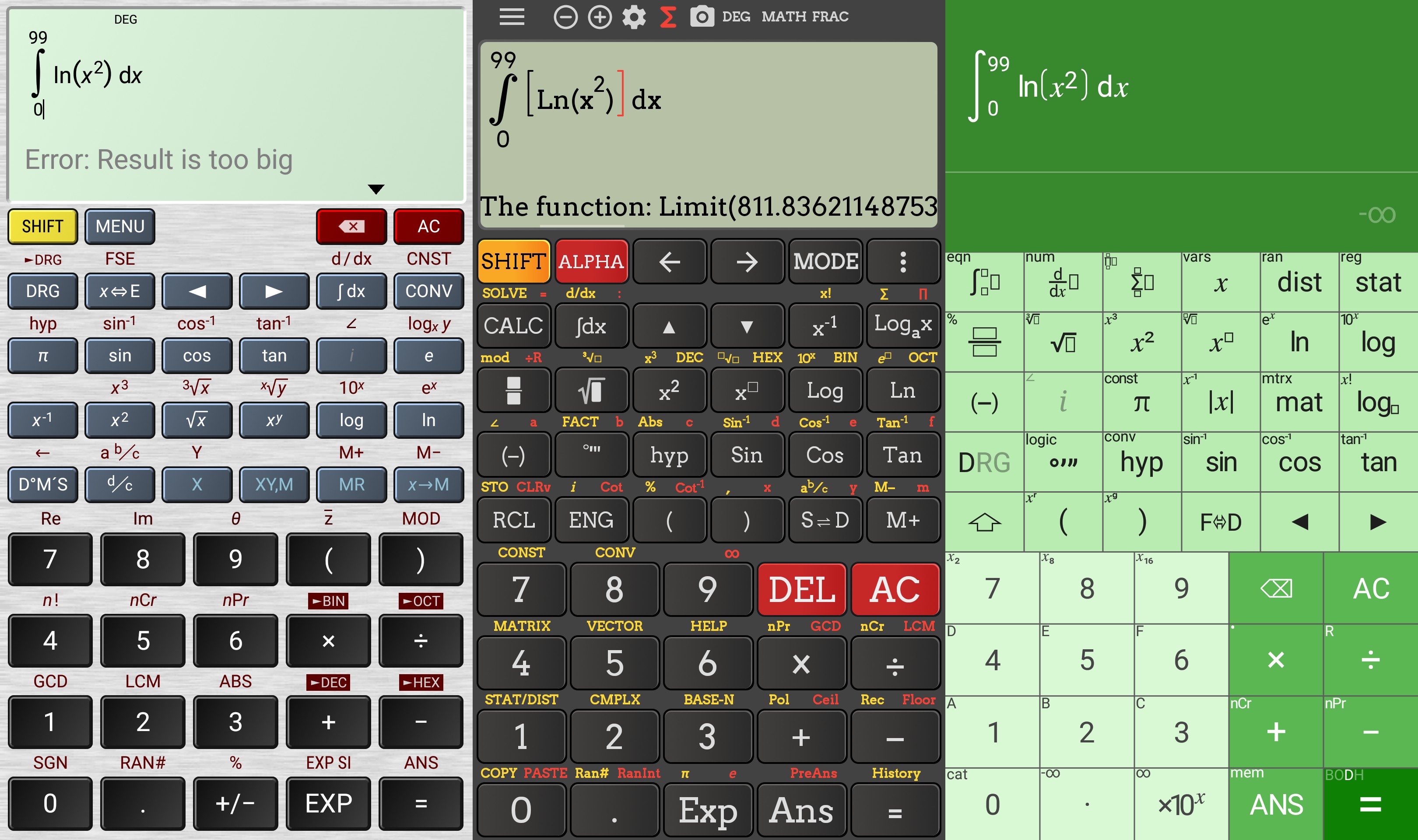
…but so do: the Vietnamese apps (in version 3.9.1) and Philip Stephens’ one! The full error text for the Vietnamese:
Math Error: org.e.c.e.a.s: The function:
Limit(811.8362114875345,89.86176729778923->99) has wrong argument
811.8362114875345 at position:2:
Limit: variable symbol for rule definition expected!
That’s strange to be able to compute on (-5, 99), but not on the sub-interval (0, 99)! In the meantime, with no Android app able to perform this calculus, the old-school silicon-and-plastic just worked:

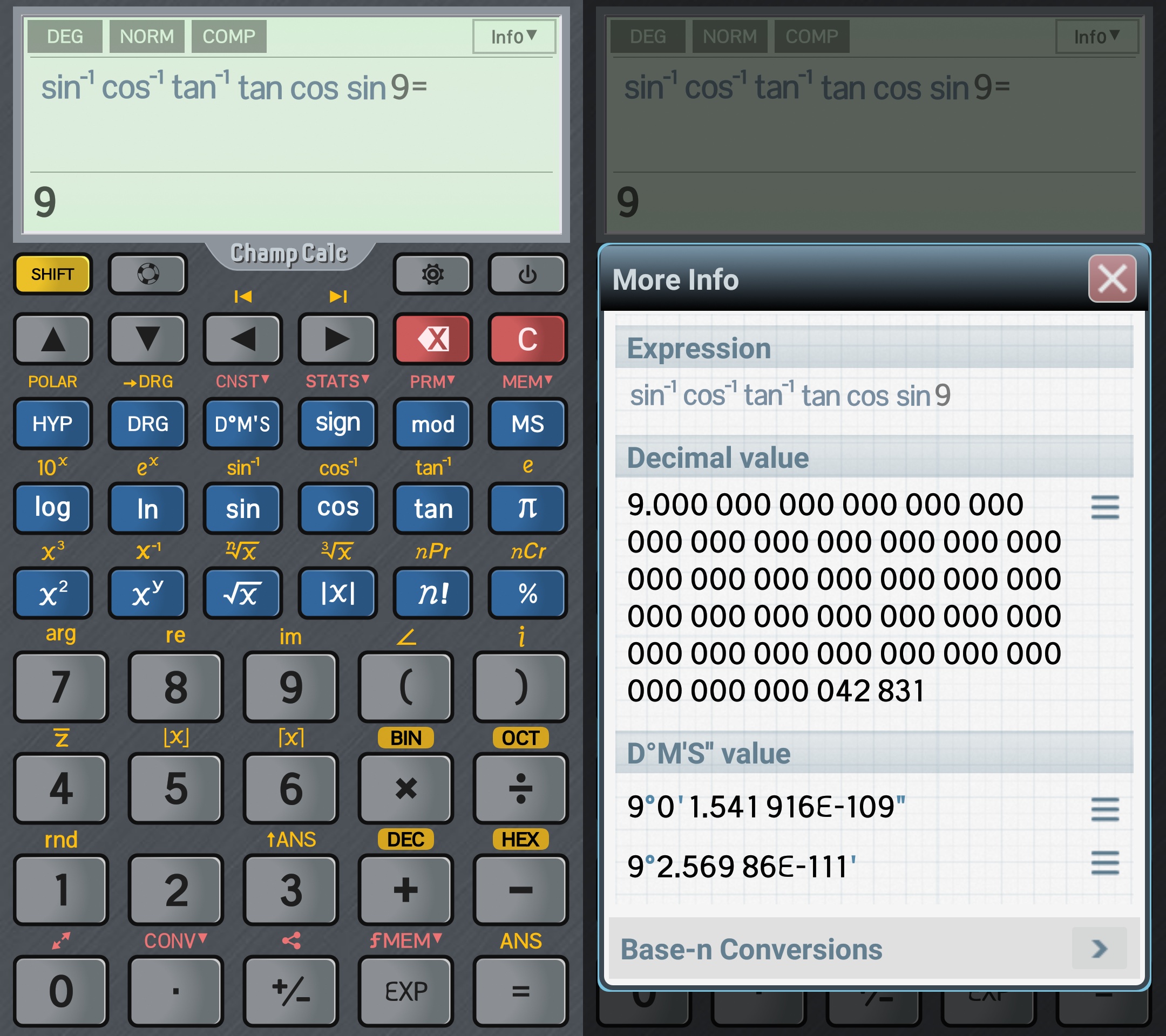
This being said, I just discovered a contender to my trusted CalcTastic Free: an app with a horrendous icon, but nice themes, ChampCalc Scientific Calculator. The free edition doesn’t have ads (just like CalcTastic), and it seems a little bit inspired from HiPER, but no integral or differential calculus and the like. The classical arcsin (arccos (arctan (tan (cos (sin (9) ) ) ) ) ) hides a teeny tiny error after 112 correct decimals!
It can be a bit slow at times, and that’s because it uses Apfloat for an arbitrary precision arithmetic library. But it hasn’t always been the case. Here’s what it was like in versions 2.02, 3.19 and 4.00. It’s starting with 4.00 that more than standard precision was offered, unfortunately not in the free version. It’s only since 5.00 that arbitrary precision became free!
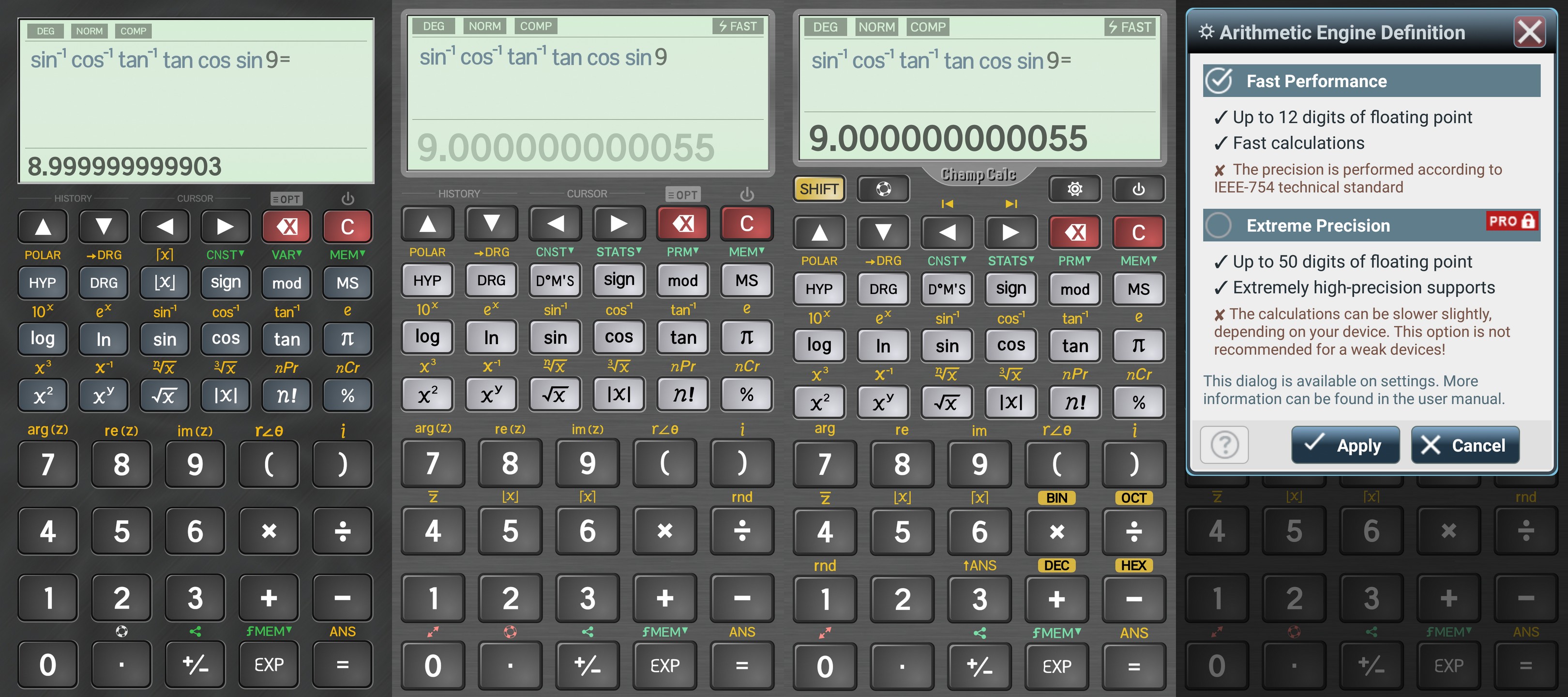
OK, since version 5 the displayed result is 9, but there are strange differences once you hit the “More” button. Versions 5.00 to 5.19 display a “pure” 9; in version 5.32 one could spot a remaining error in the D°M’S” field (e-45); 5.41 started to show the full number, no questions asked; 5.42 dropped the last two digits (42831 instead of 4283132).
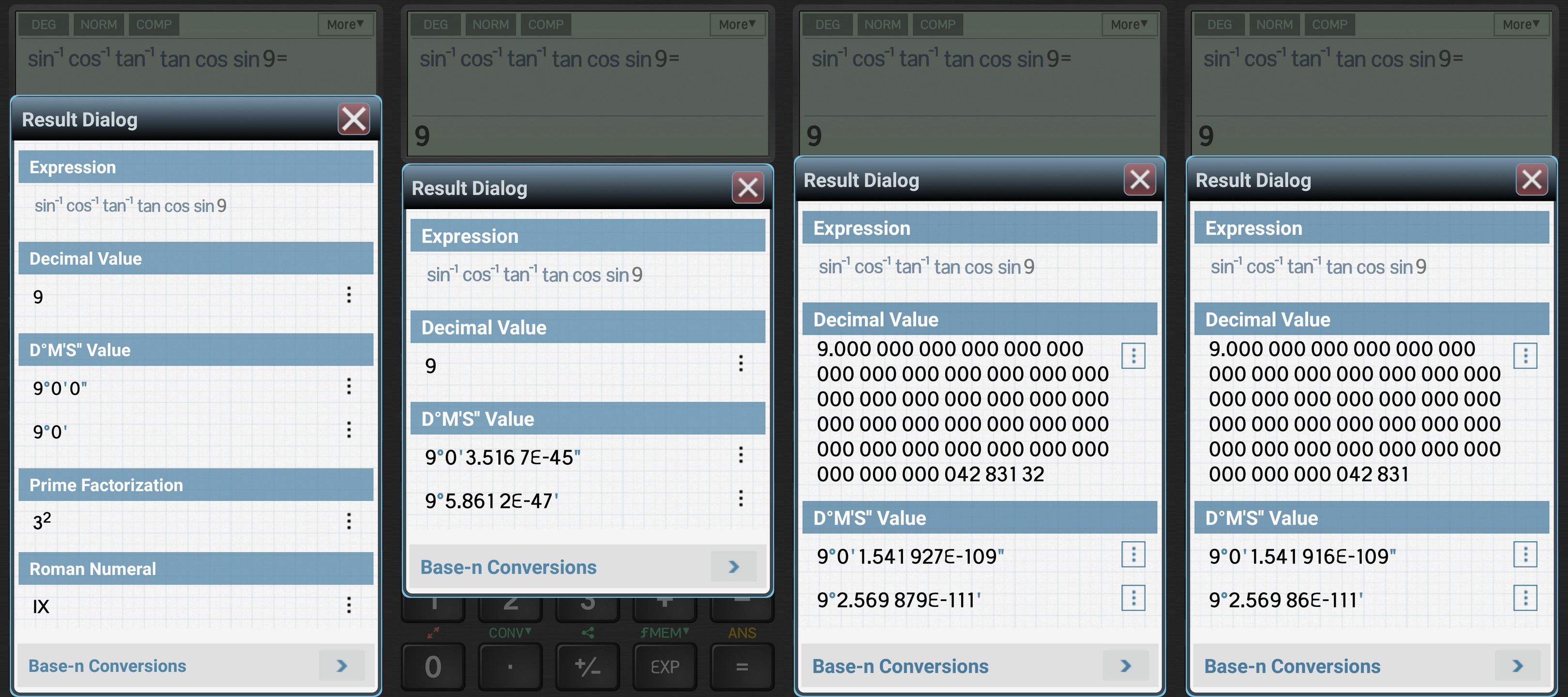
Since 5.43 (including the current 5.45), one has to tap on “More digits” to see the whole string; and yet, D°M’S” betrays it…
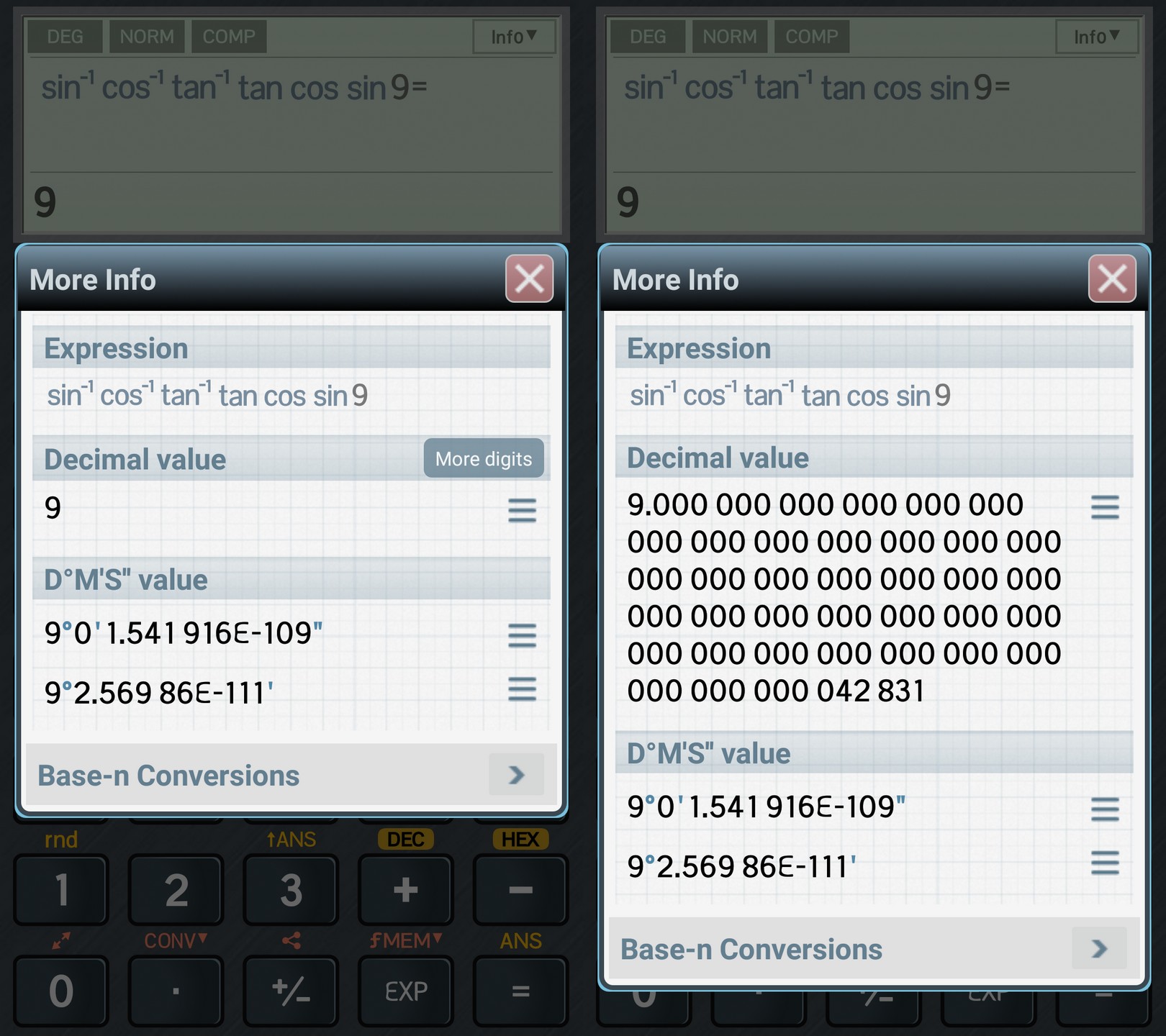
One more strange thing with ChampCalc. In versions 5.00 through 5.34, I noticed it uses a class BigDecimalMath in which, among other things, it stored (I’m not kidding!): e with 1404 digits, pi with 1638 digits, gamma (Euler-Mascheroni) with 1482 digits, and ln(2) with 1638 digits. At the same time and for some other uses, BigDecimalMath stores a few pathetic BCD (binary-coded decimal) approximations of pi: 0x400921f9f01b866eL (3.14159), 0x400921ff2e48e8a7L (3.1416), 0x40091eb851eb851fL (3.14). I can’t figure out the logic of all this.
Since 5.41 (probably since 5.40), after a refactoring, there’s nothing of the kind in BigDecimalMath, but BigComplexMath stores pi as 3.141592653589793. And that’s all. How does ChampCalc know the following constants with 118 digits? (I couldn’t find them in Apfloat’s source.)
I don’t know what to make of an app whose internals change so often and so illogically: how about the bugs and regressions?
UPDATE 11–more from Vietnam! So far I kept mentioning 13 Vietnamese apps of a same author, mischievously split between several developer accounts, and bearing chaotic, stupid names. Here’s one more product of Vietnam: HiEdu Scientific Calculator!
There must be a thing in Vietnam with their obsession passion for Casio (in this case, fx-570VN Plus, which is smarter than fx-570ES Plus). They like them so much that Vietnam is a huge market of fake Casio calculators; as a result, special holograms “with German technology” have been created specially for Vietnam!
Back to the app now. Since I tested other apps not just for accuracy (typically higher than with a physical calculator), but also to find pathetic failures (usually with integrals) let’s test HiEdu a bit.
As we’re contemplating the first failure (should have read 717.928…), let’s note that it’s impossible to know the 2nd and 3rd functions of a button until you press Shift and Alpha:
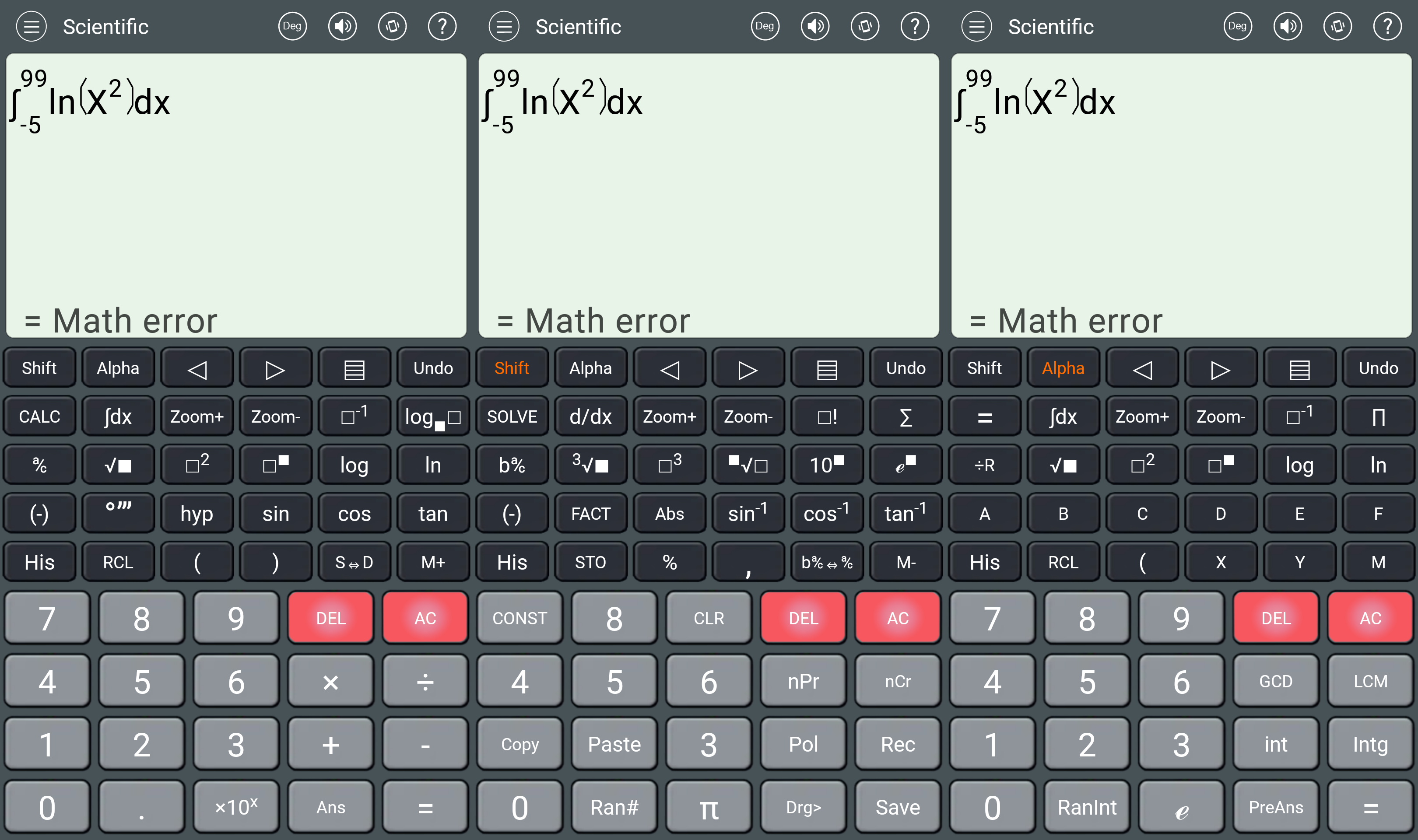
OK, let’s investigate. Is it the wrong minus sign (the “(-)” one) or the wrong “X”? No, it isn’t (see the result 4888). Is it about negative numbers? (Nope, 0 still crashes it.) Oh, wait, it works for start values slightly over zero! (Yes, I know that ln(0) = -infinity. But it’s actually a limit.)
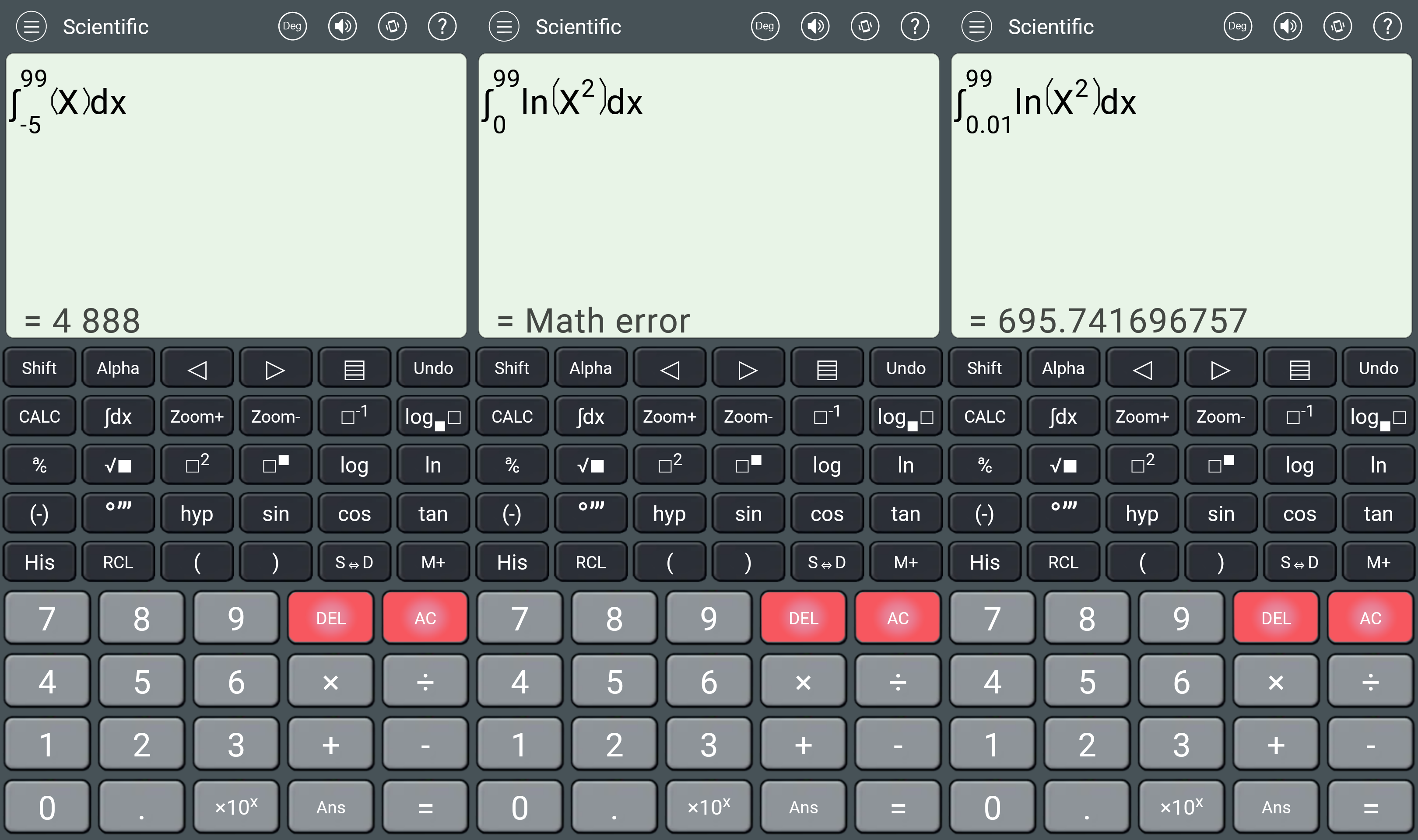
I’m really sick of such misbehaving apps. (On a positive note, the unit converter is quite practical, and the programmer’s layout is useful as long as you don’t want to shift bits.)
LATE EDIT: There’s now also a paid edition, HiEdu Scientific Calculator Pro, in which the 2nd (Shift) and 3rd (Alpha) functions no longer need to be guessed. But the Solve button prints “Solove” (the settings area is in Vietglish: “… will fomatted to …”) and arcsin (arccos (arctan (tan (cos (sin (9) ) ) ) ) ) gives 8.99999999983257 on maximum precision (30 digits), although the reverse order of trigonometrical functions resolve to 9 (physical calculators typically behave the other way around):
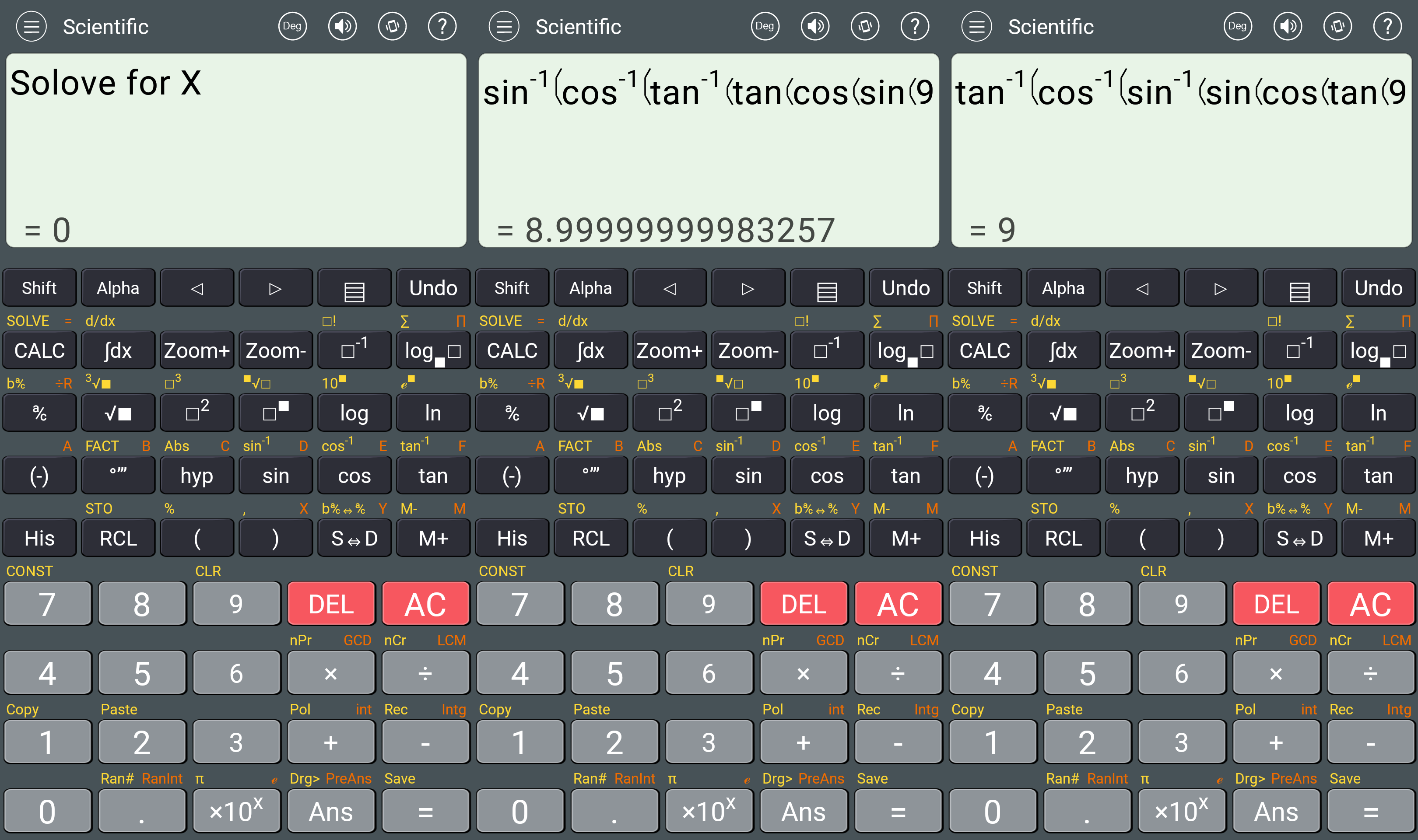
I have tried too many apps and they all suck. Sure thing, for everyday use–that is, no integral calculus or other sophistication–any skeuomorphic app that’s well designed should fit, including the tried and trusted CalcTastic, or maybe ChampCalc. But for some real engineering calculus, there’s no app that wouldn’t stupidly fail where it shouldn’t! GUI design aside, Philip Stephens’ Scientific Calculator has everything scientific and engineering at hand, but it has precision issues and while integrating near zero, it really tries ln(0). OK, let’s try simpler:
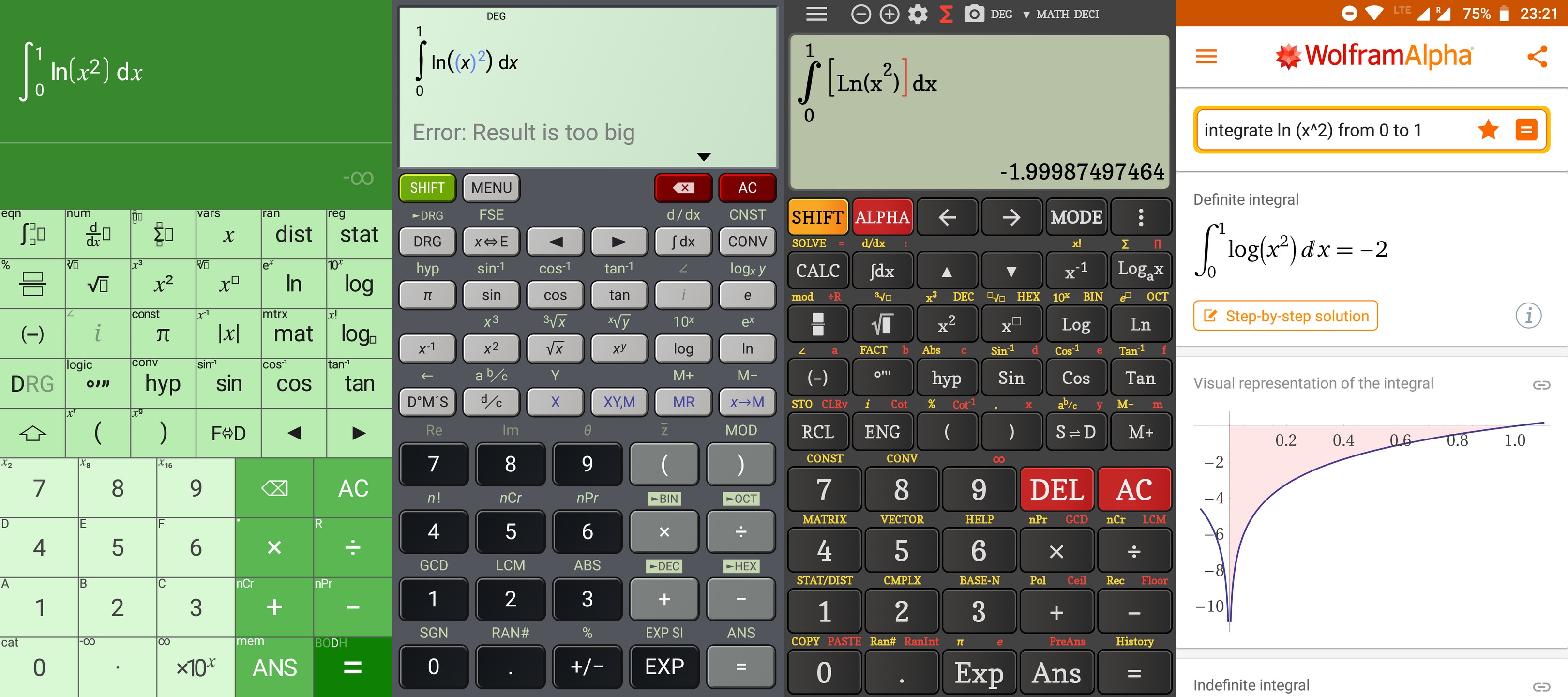
I’m back to square zero. Stupid silicon and bits. That’s the difference between approximating and solving a fucking integral.

UPDATE 12, updated–the fun (is it obsession?) goes on! In the meantime, the 13 Vietnamese apps got updated to version 3.9.3, and I tested four six of them. Philip Stephens’ Scientific Calculator went from 8.40 to 8.70 without visible changes.
Let’s start with the good news: some fixes in the Vietnamese flock. The sum that failed and the logarithm that failed (see UPDATE 9) now work (although 711.846… is slightly off the correct 711.833…):
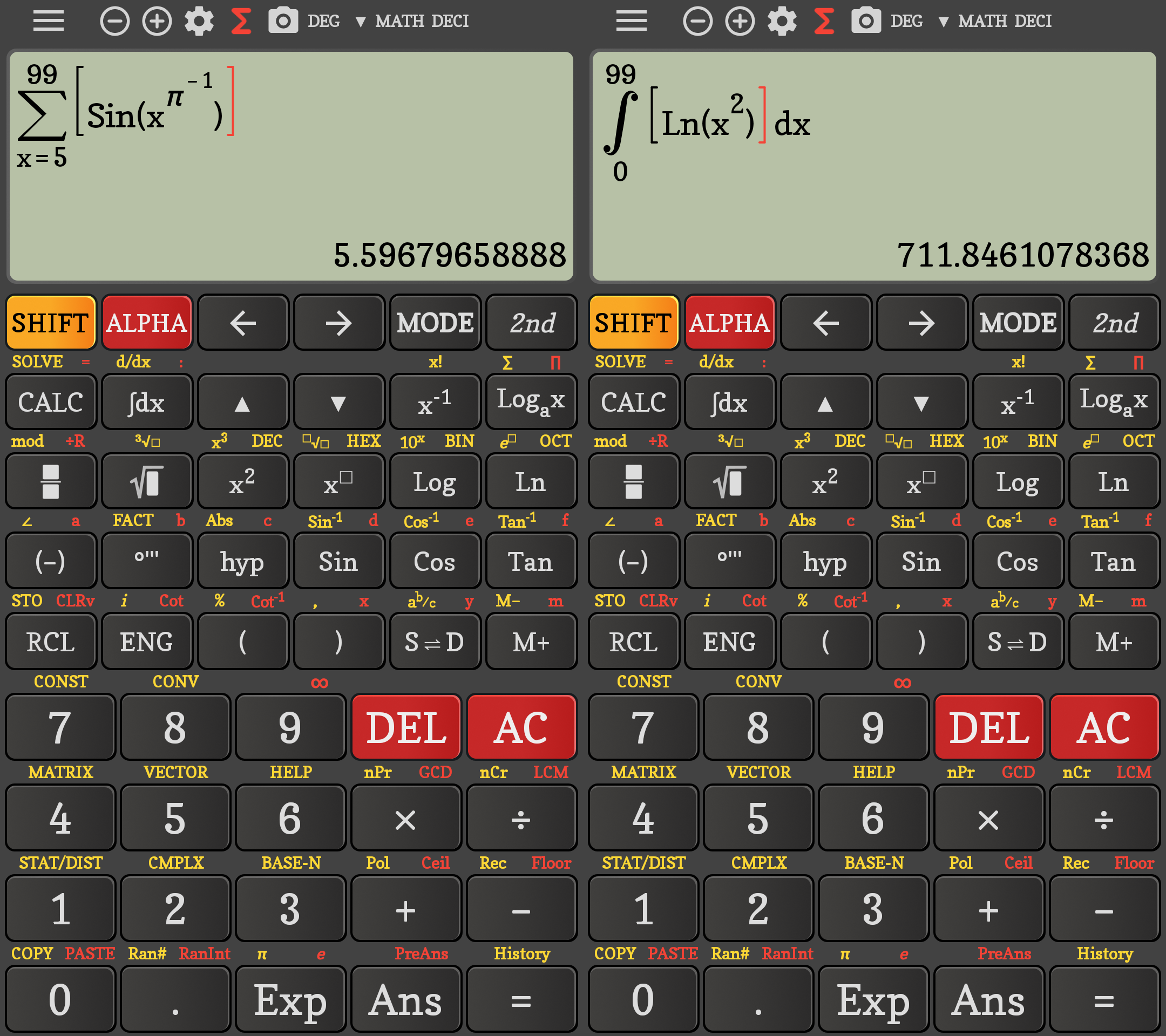
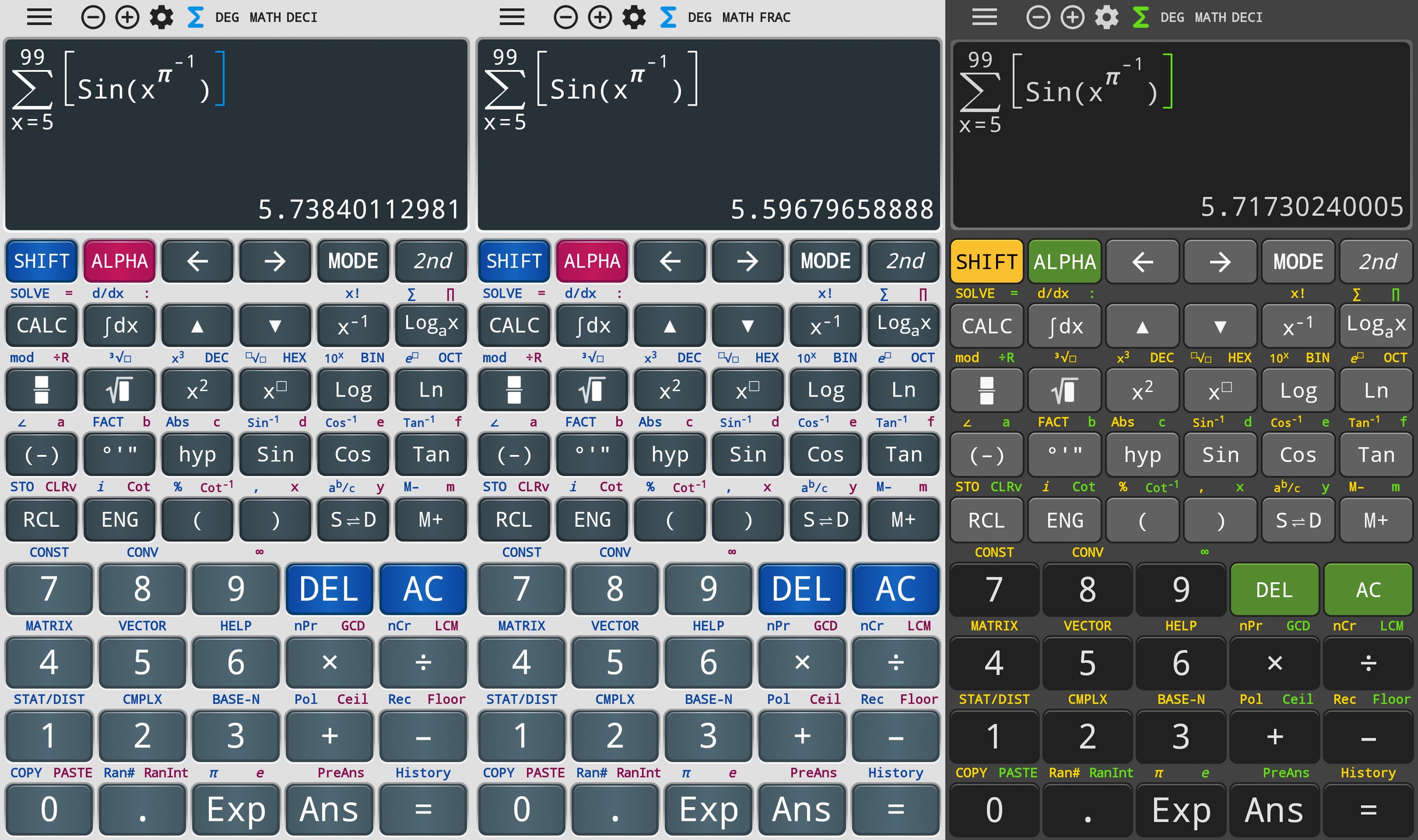
In some cases it can even solve them (toggle with S/D):
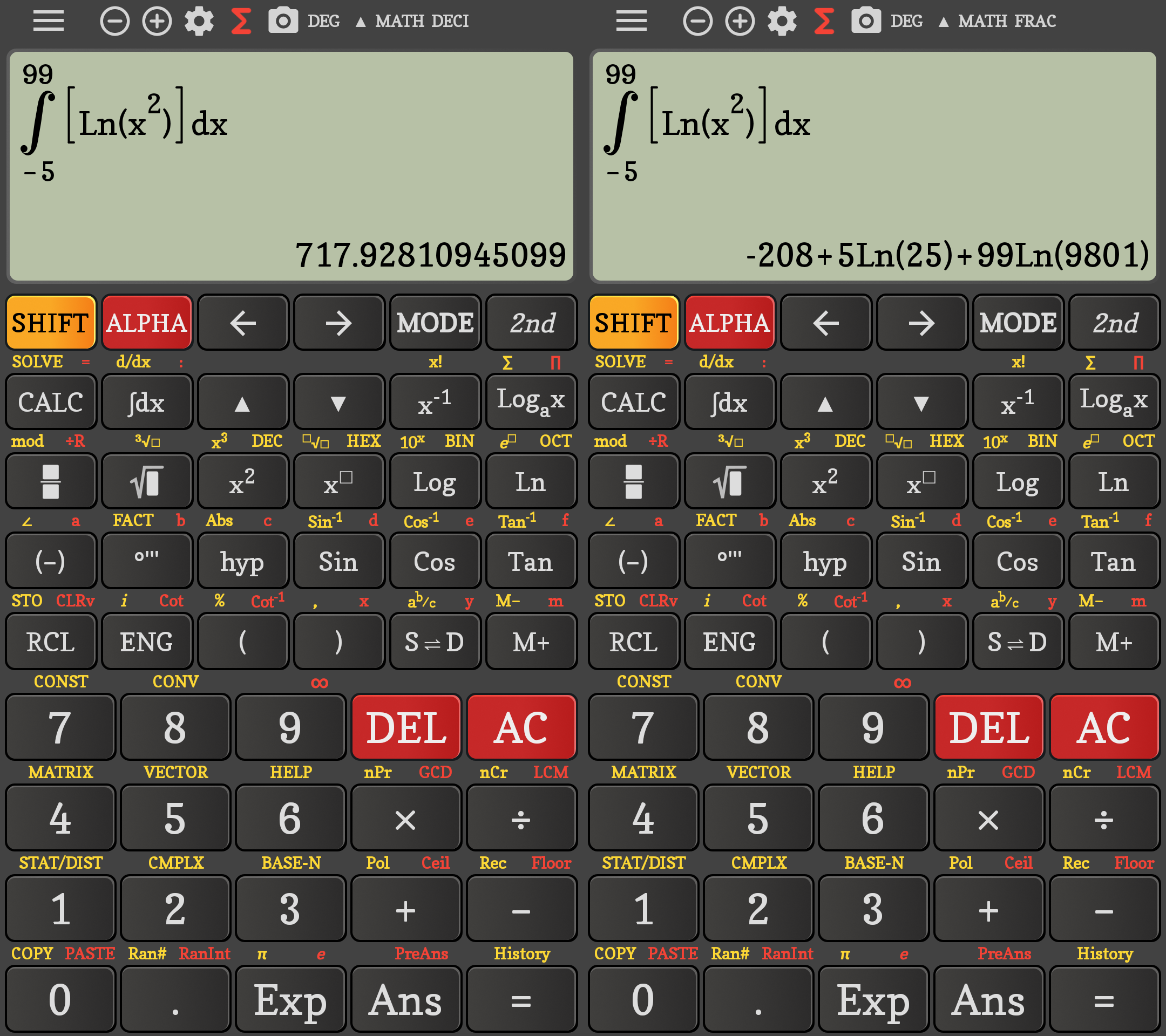
The above were tested in com.tool.calculator.casio.fx991.es.plus (icon label “991 ES”) and com.mrduy.calc.ti36 (icon label “TI-36)”. But com.nstudio.calc.casio.business (icon label “Calc Business”) only got new bugs; first, the integral fails with a different error than before:
Math Error: org.e.c.e.a.s: The function: Limit(98*Log(9604),98->99) has wrong argument 98*Log(9604) at position:2:
Limit: variable symbol for rule definition expected!
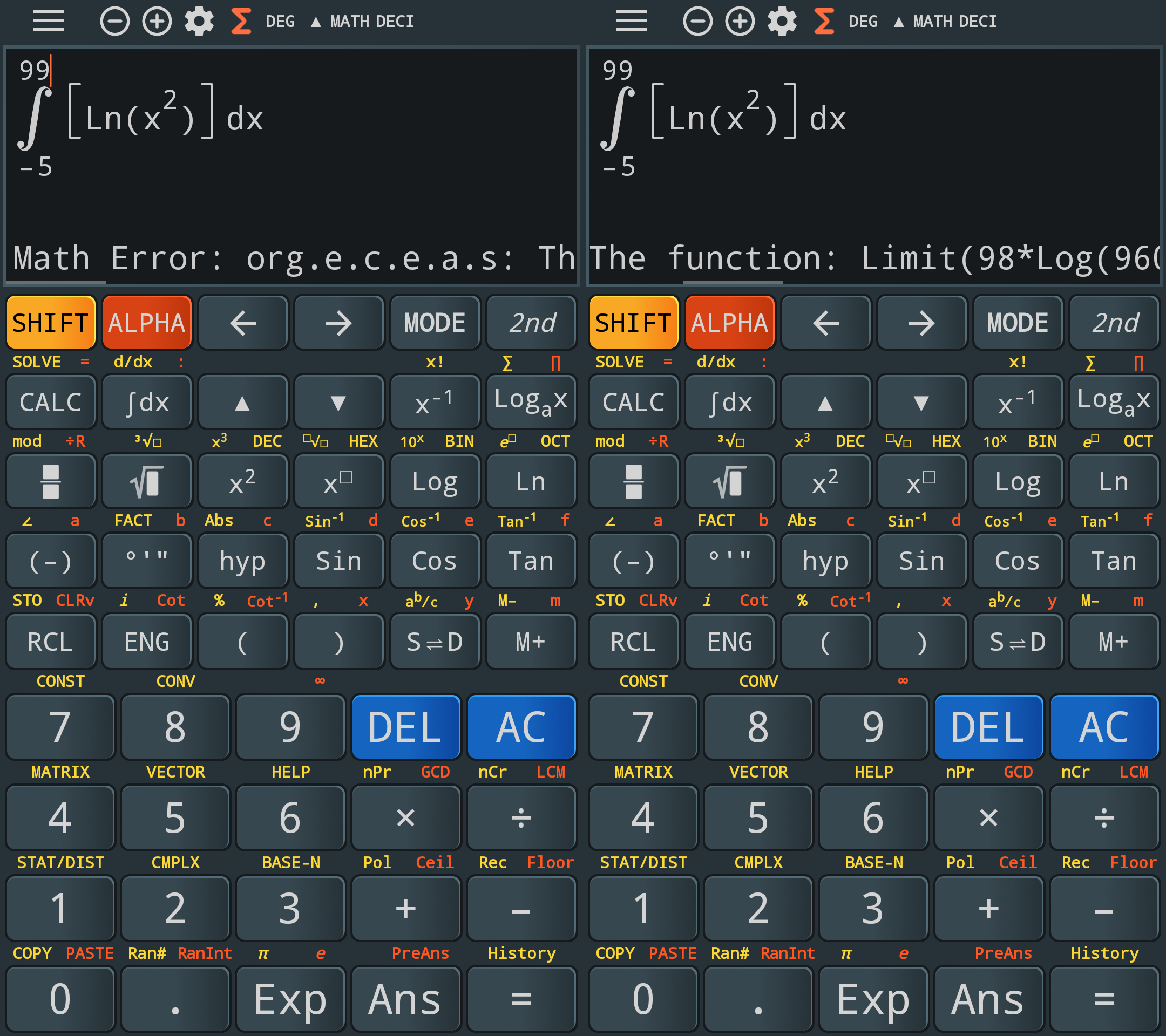
Then, the sum that now works can give different results, depending on whether you’re in fraction (5.698…) or decimal mode (5.693…), but playing around again in fraction mode the correct (5.596…) is eventually obtained… but this is purely random behavior!
com.nstudio.calc.casio.modern (“Calc Modern”) and com.nstudio.calc.casio.tavern (“Calc Tavern”) fail for the integral at different points than “Calc Business”:
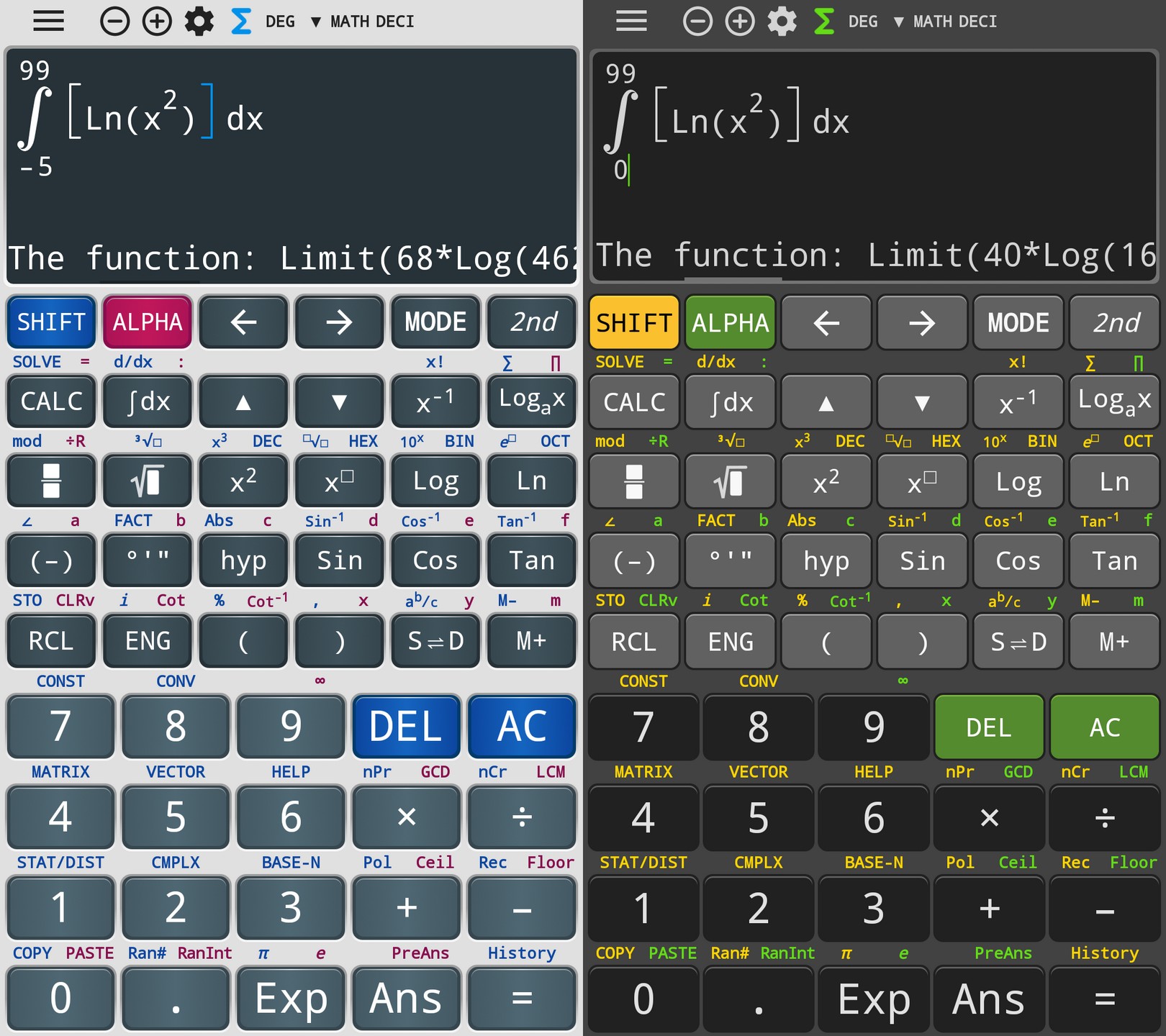
The 5.596… sum can have different random values:
Back to “Calc Business”. More random fuckups with indefinite integrals (2nd screen of buttons); the correct answer is in the last screen (“991 ES”):
More random values with “Calc Modern” and “Calc Tavern”:
That was truly astounding!
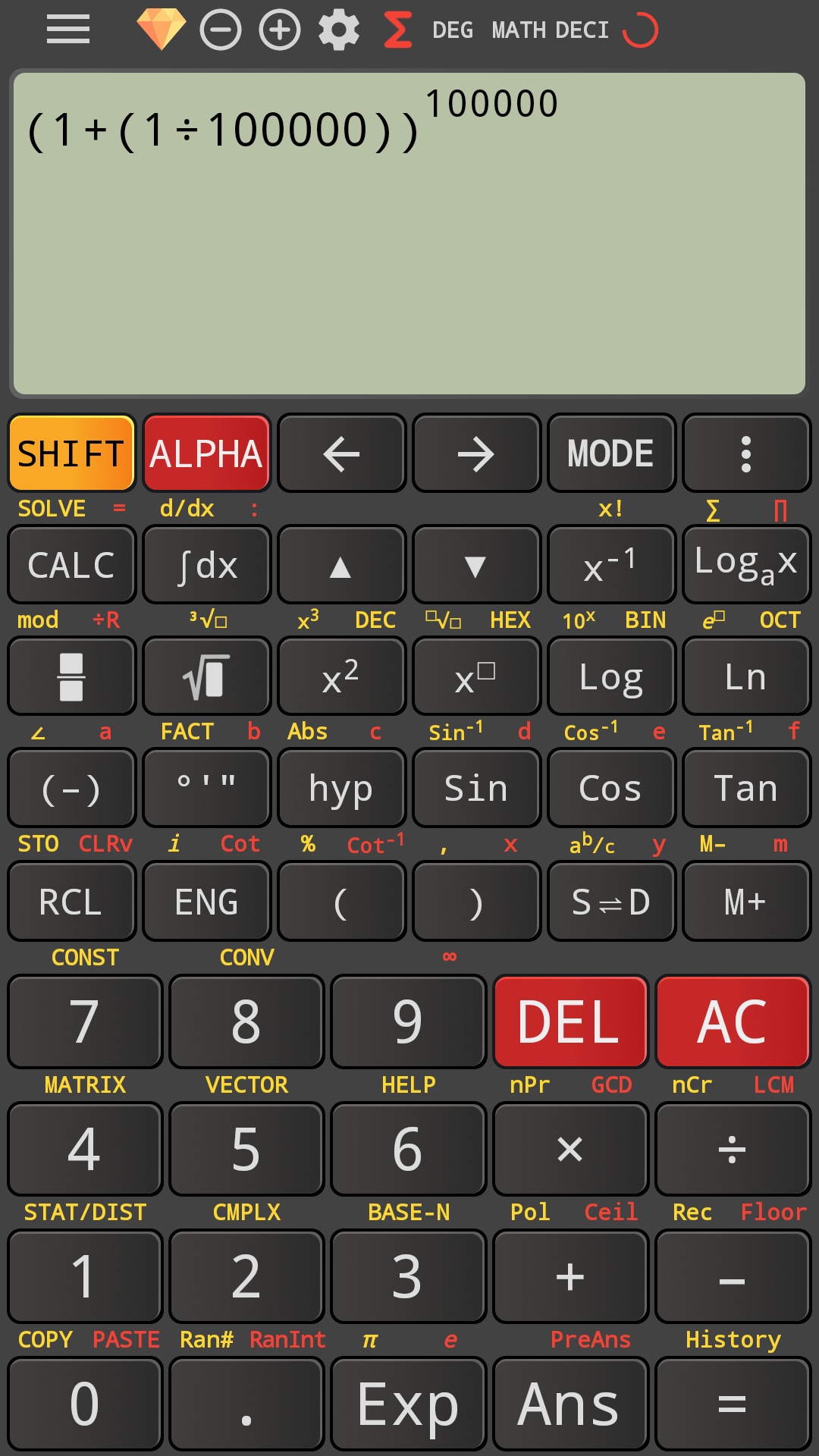
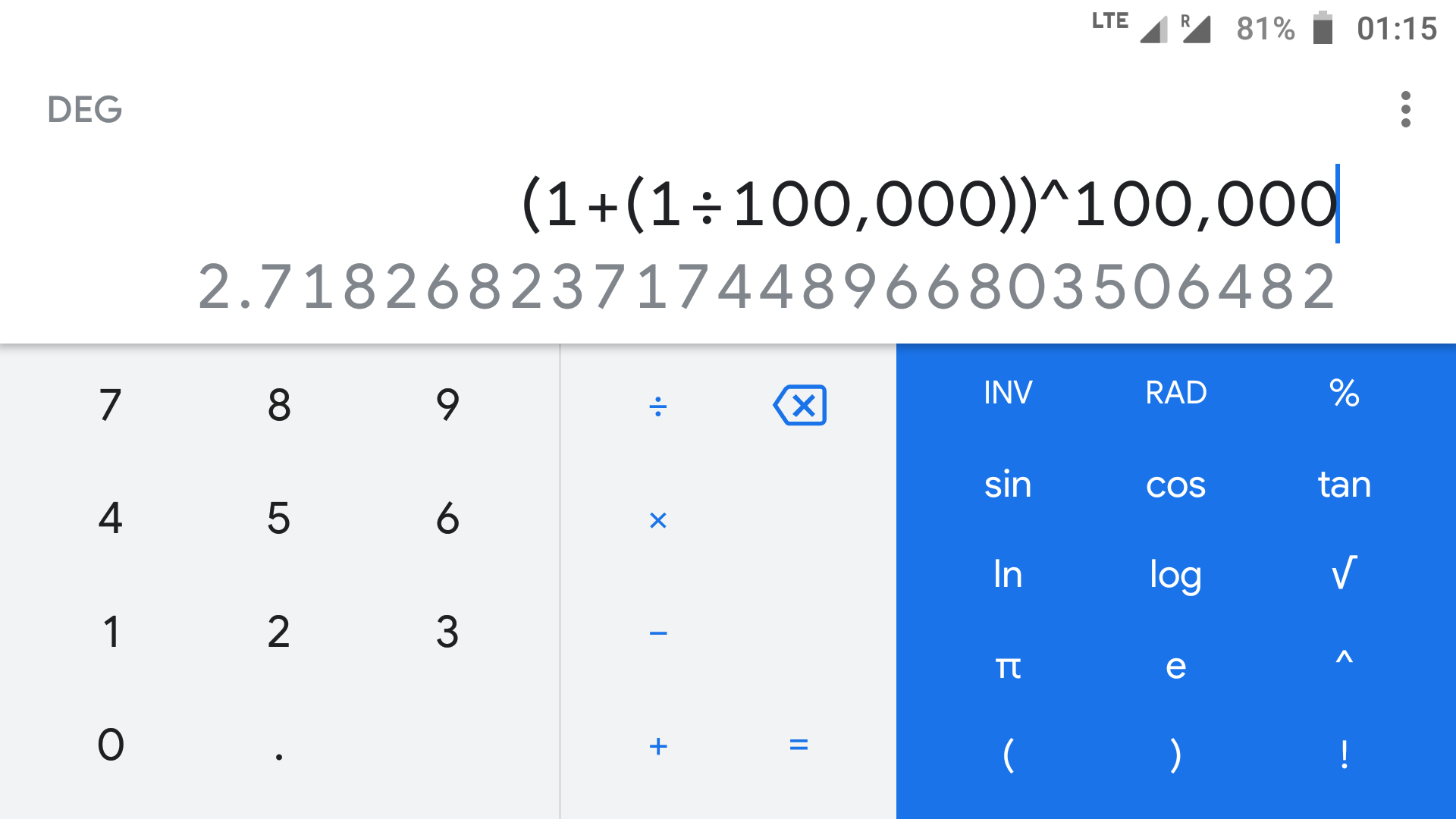
Back to “991 ES”, here’s a product that freezes just like the unsolved (1+(1/100000))^100000; if 99 is too much, it gives the right answer for 9, and then changing it back to 99… a random value pops up!
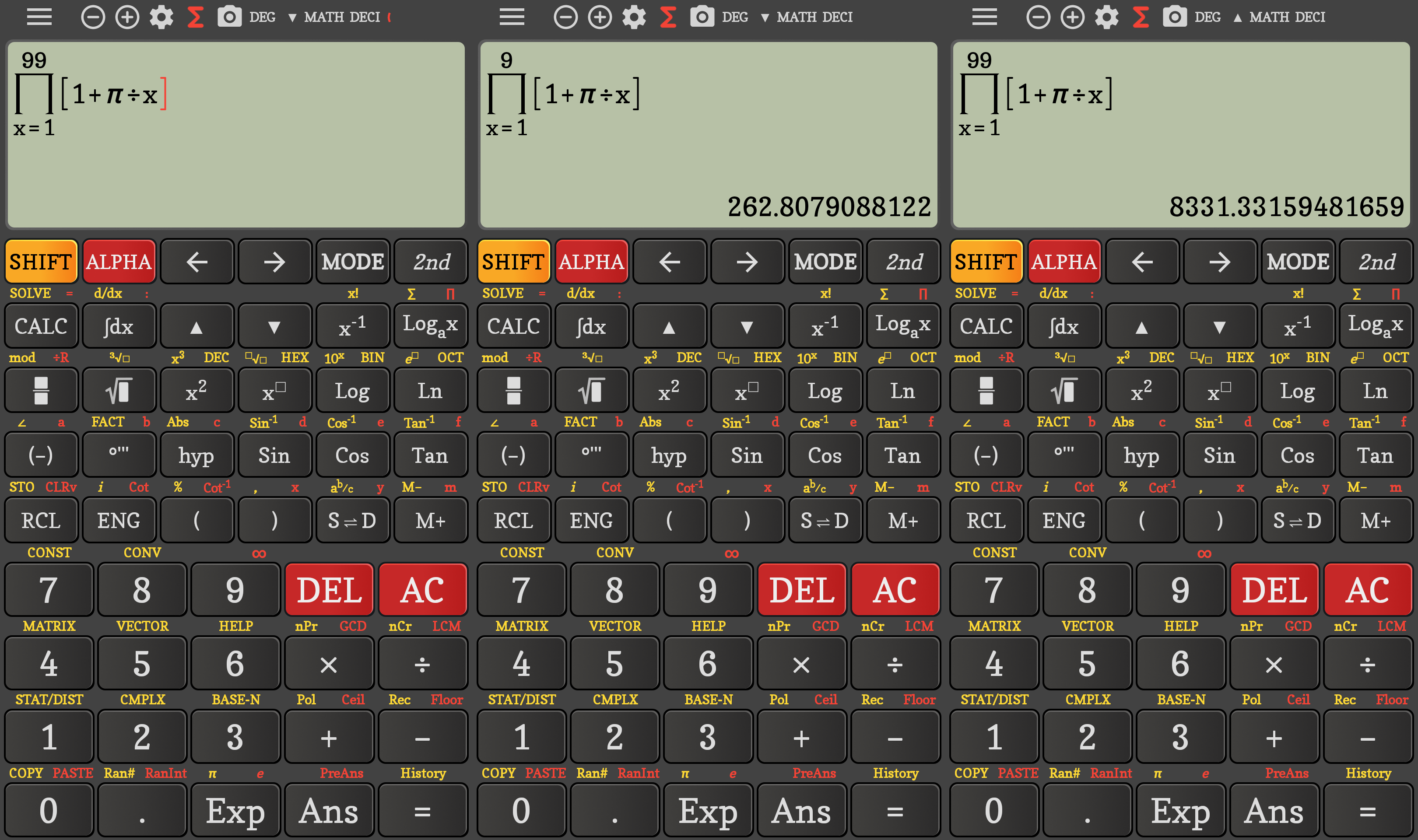
For once “Calc Modern” is correct, but “Calc Tavern” tries to be original:
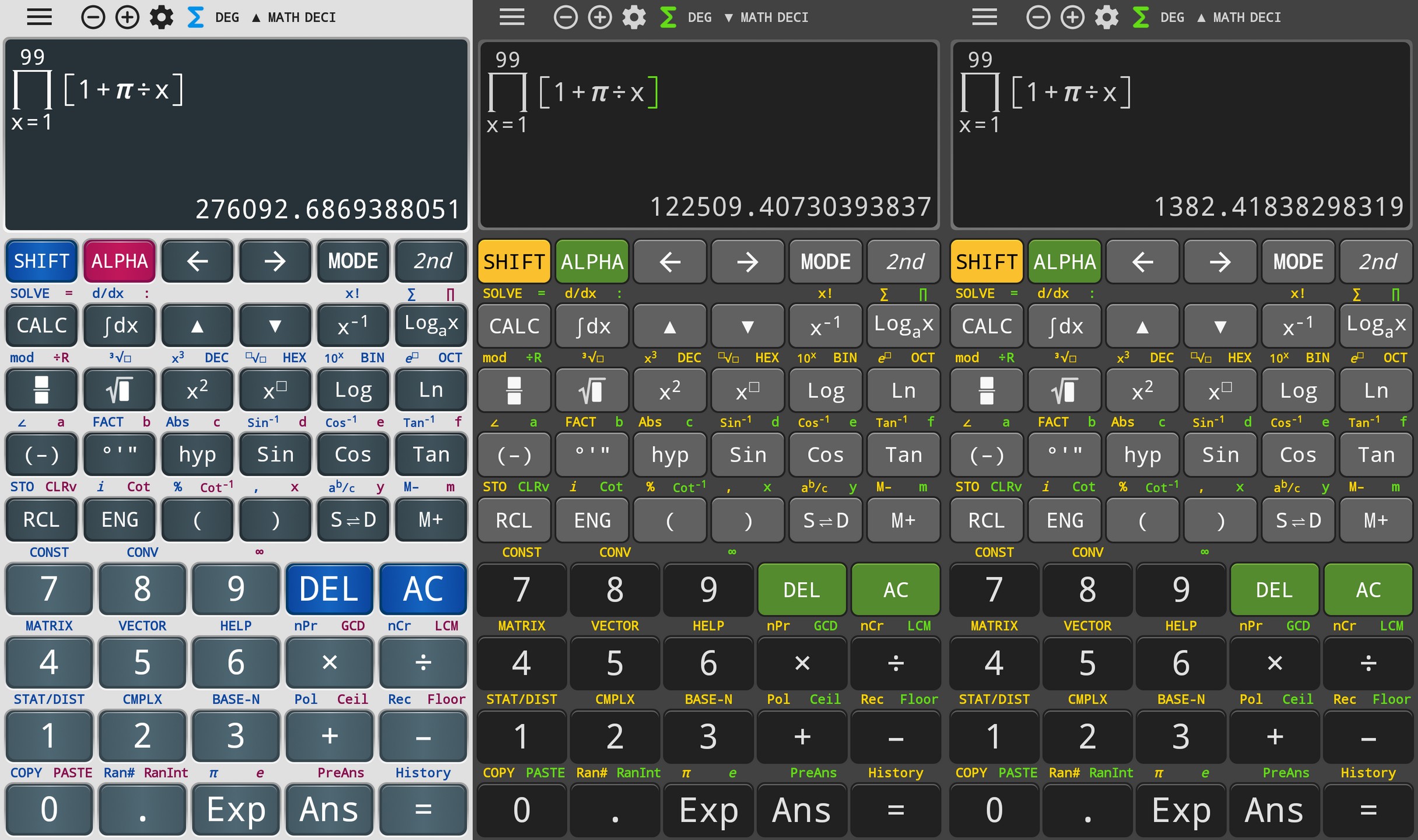
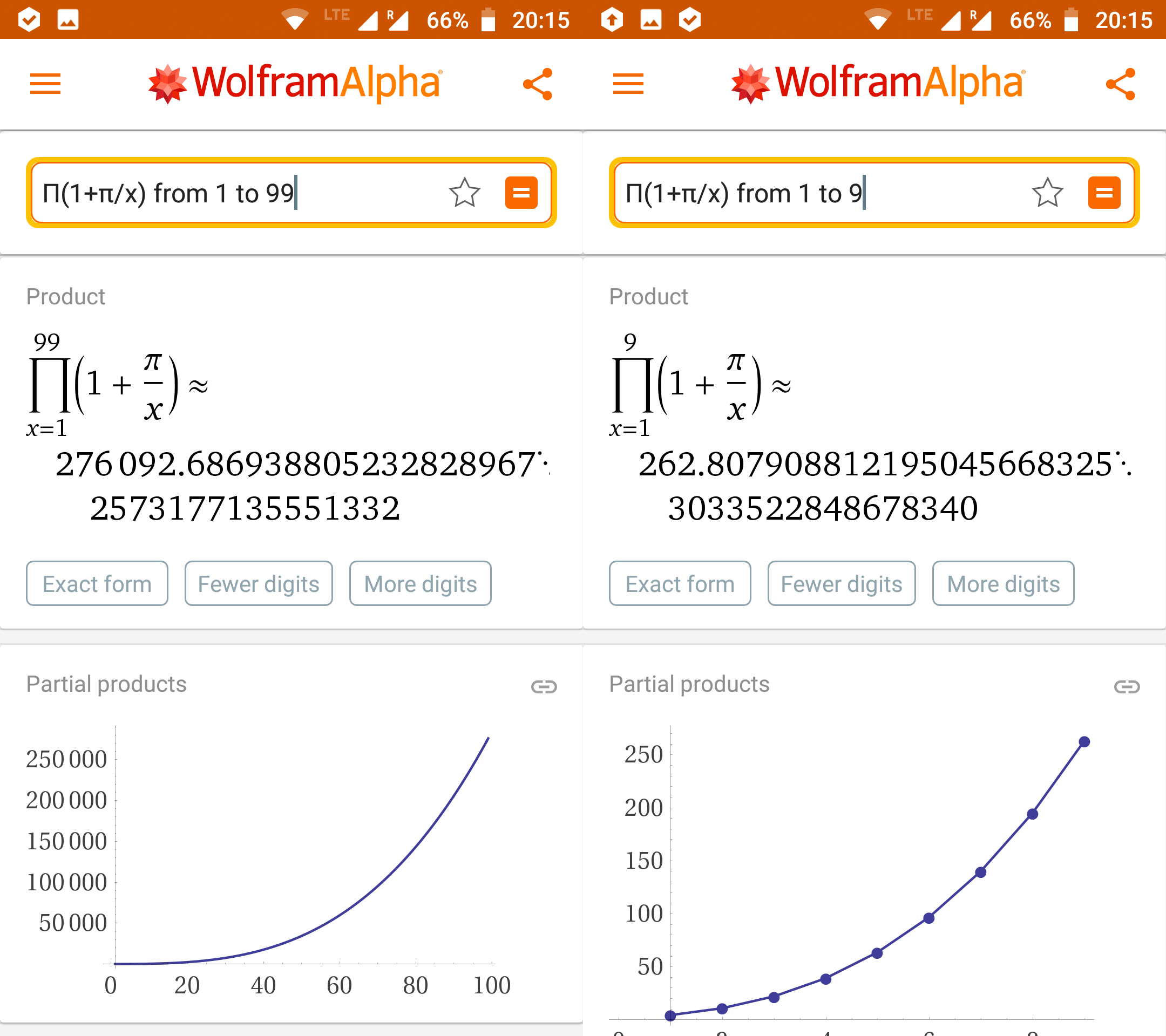
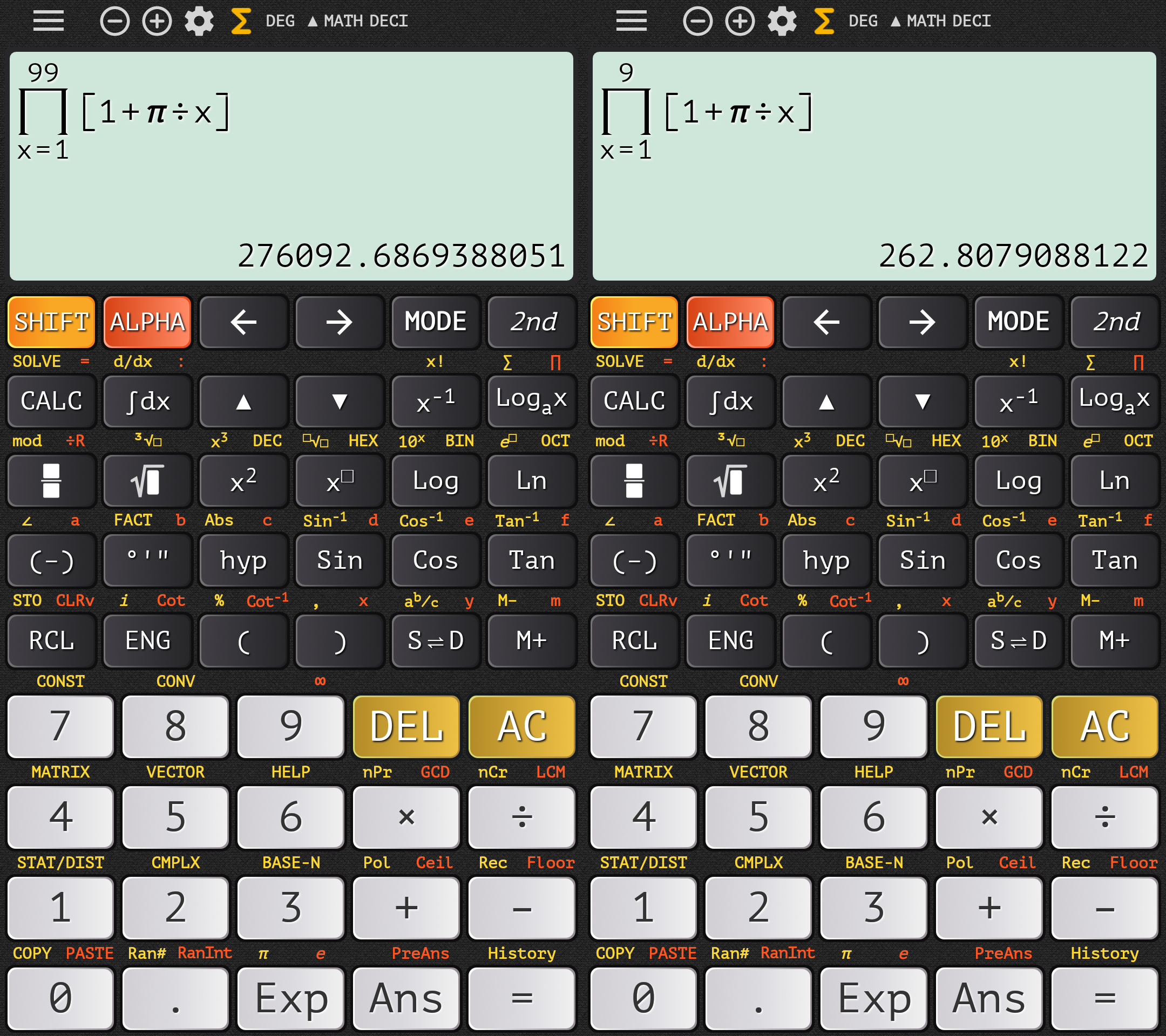
For the curious, the correct value for 99 is 276092.6869…:
HiEdu also fails with 99 but works with 9:
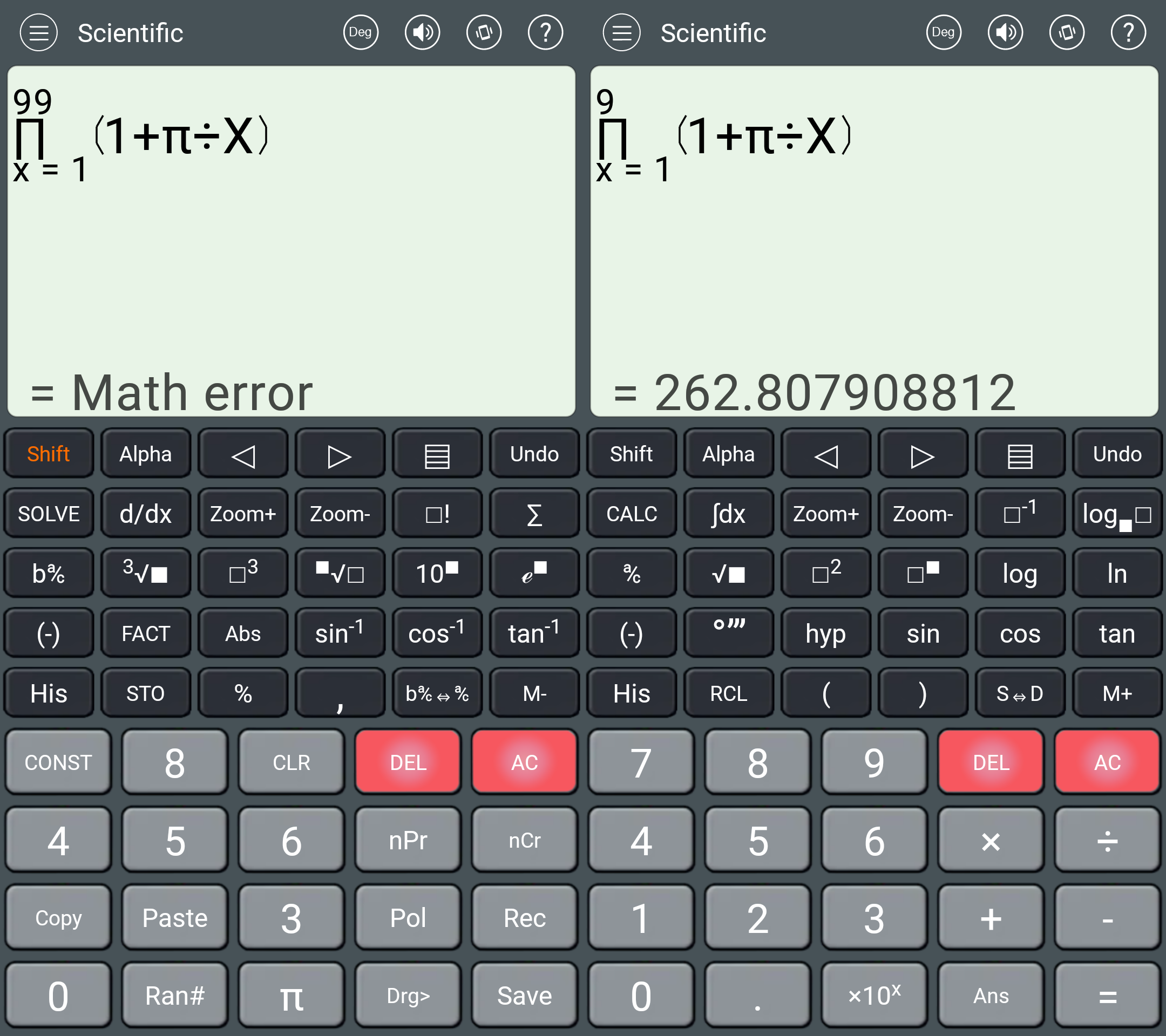
Philip Stephens can solve both of them correctly!

Unfortunately, no improvement on the integral side: still 717.969… instead of 717.928…; from 0 it still fails with logarithms, and trying tiny shifts such as 1e-99 gives important errors, here 704.493… instead of 711.833…

How about anotheer Vietnamese app upgraded to 3.9.3, namely com.calculator.tool.fx350ex (icon label “Fx 350”)? Well, it’s another mess. First, definite integrals fail, indefinite integrals give random answers…
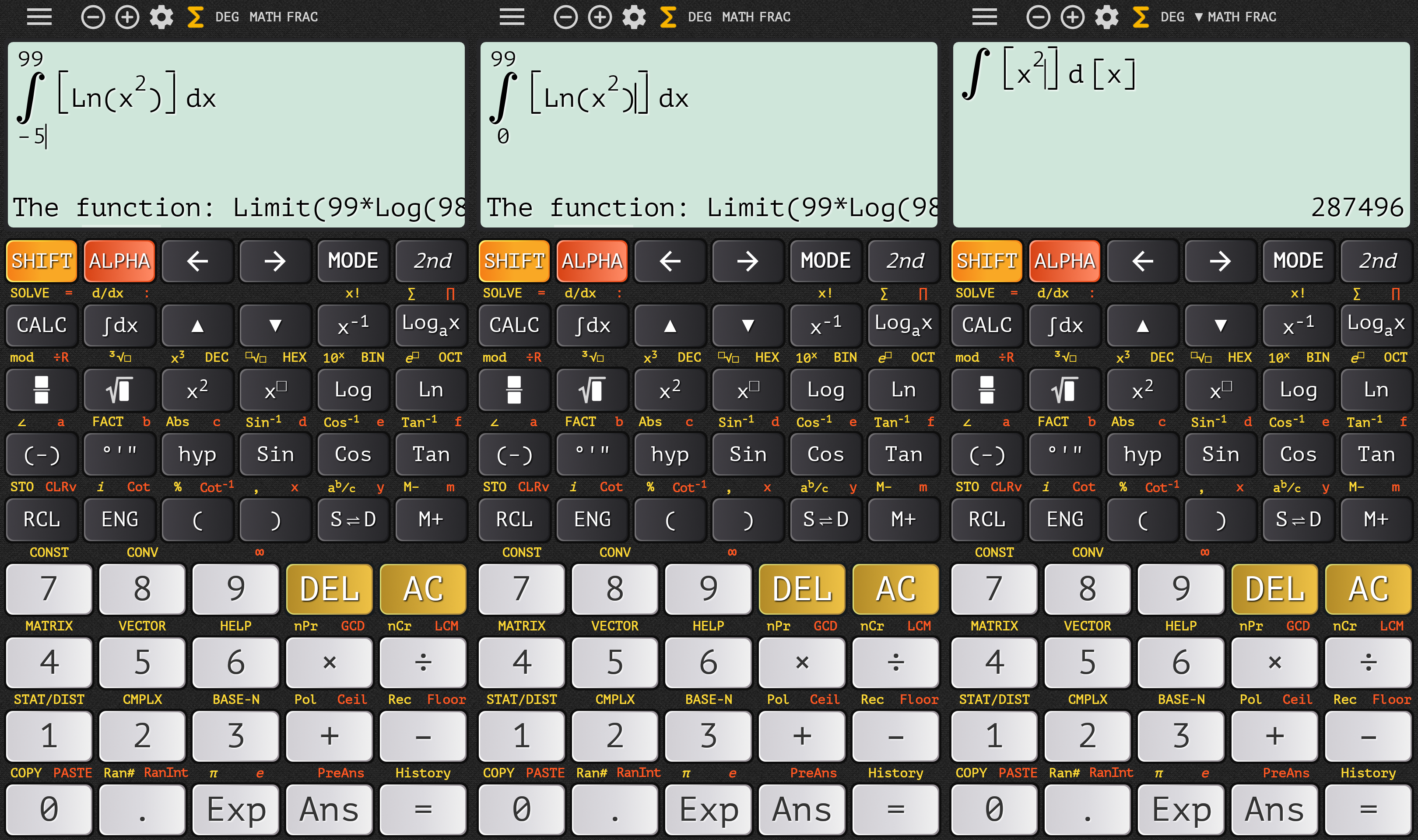
…then the bloody sum that can havee random answers now can have one of them the correct one with further decimals…
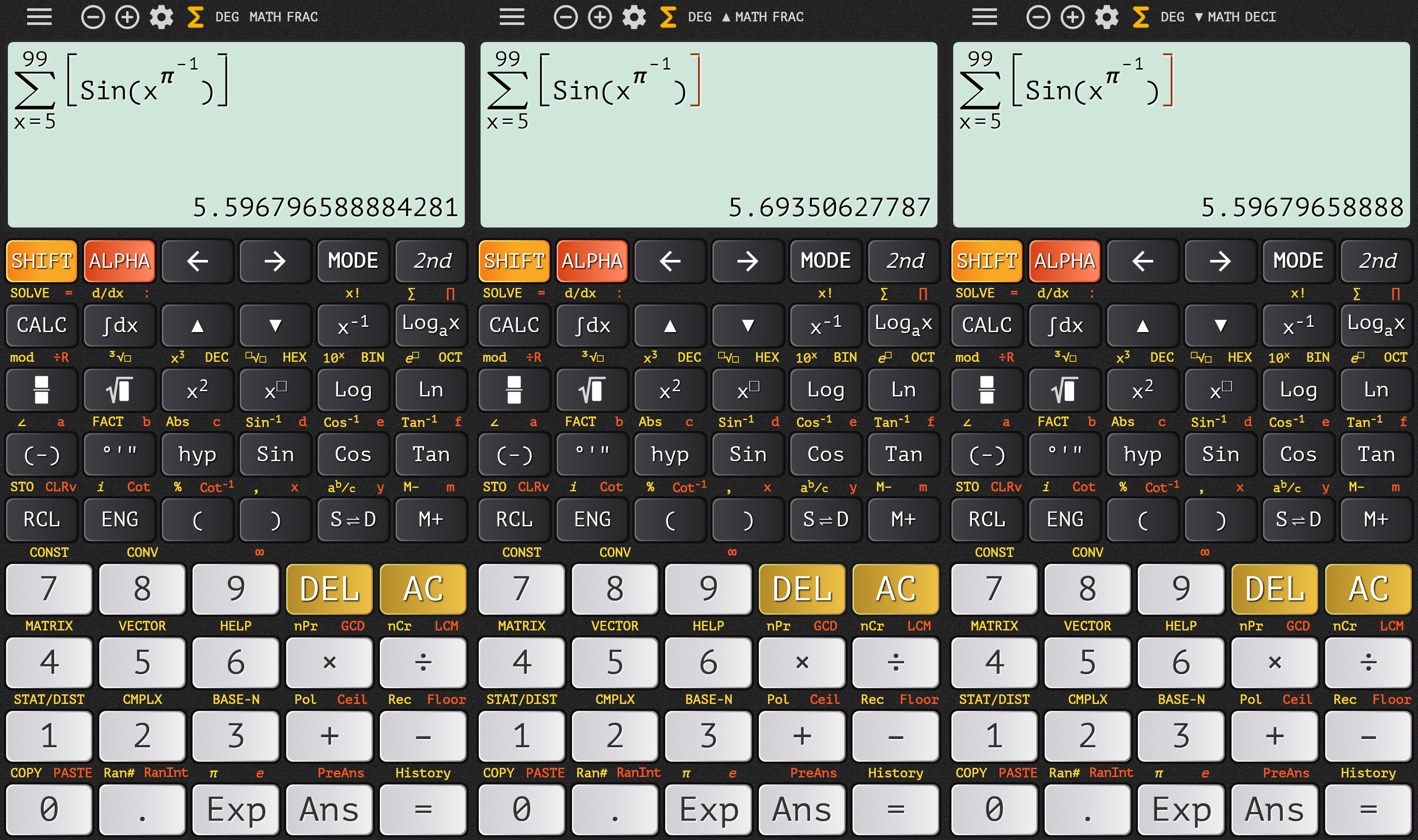
…but it can solve the product even for 99!
As a last attempt to check again other siblings, no luck with “TI-36” and “Calc Business” (they still froze), but “991 ES” managed to issue a random result, yay!
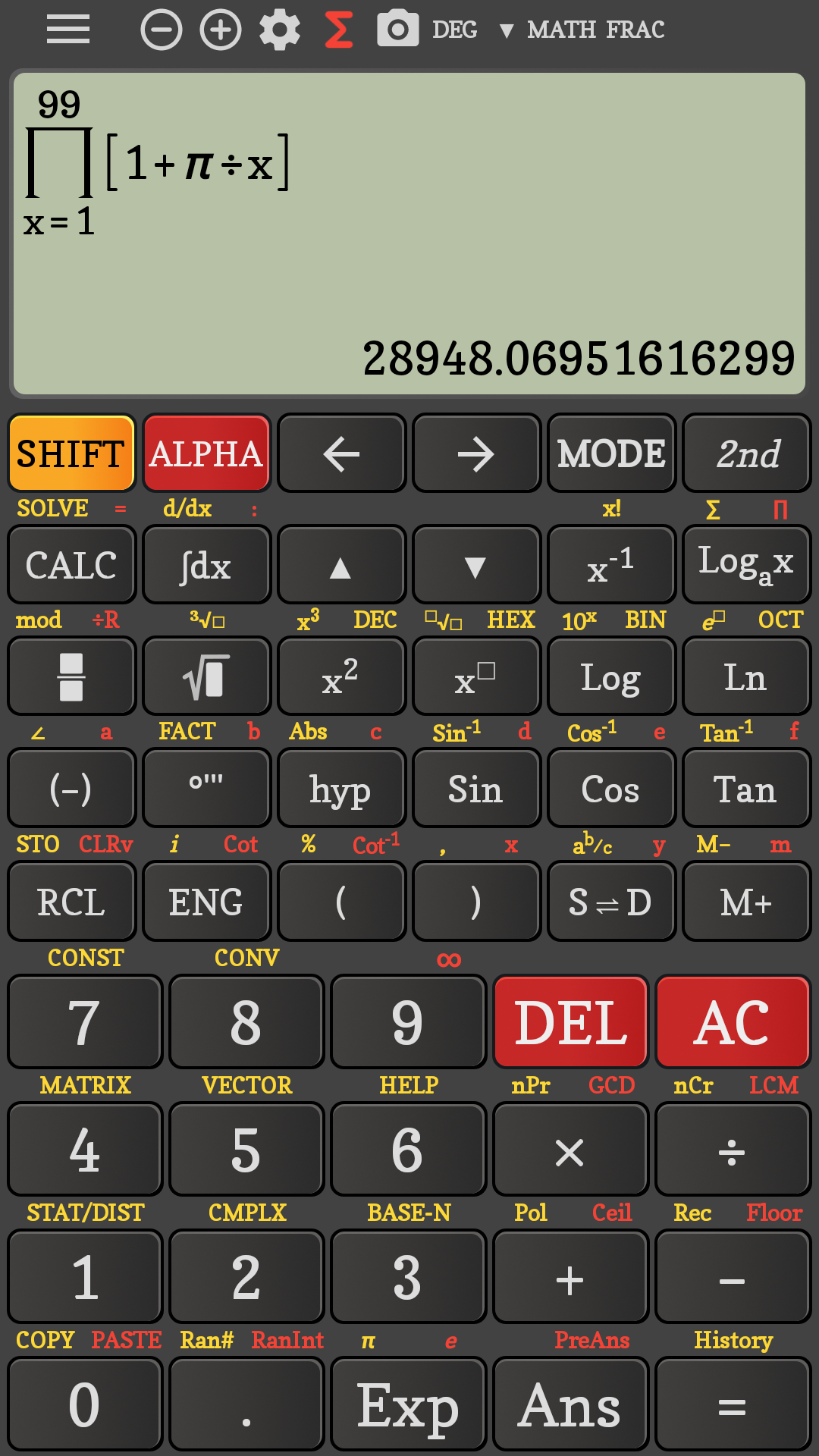
Just how much fucked can a software be? How could anyone use something that gives random results for anything that involves repeated calculus? To understand the magnitude of the issue, these 13 apps of a same developer (that’s pure greed to release 13 clones instead of focusing on making one good app!) are offering so many functions that they needed two screens of buttons, and the bottom rows on the second screen are menus that include many different functions each! Would you trust their accuracy, or are you just willing to accept any random result?
The pervert thing is that nothing on the second screen can be used in the free version! OK, exit the indefinite integrals and derivatives, but in order to use the definite ones from the first screen, one has to enter “x”… which is on the second screen and thus cannot be used! Same for sums and products, which also need an “x” variable…
The best placement of the buttons is in Philip Stephens’s calculator, too bad the precision is… too approximate for “too scientific” calculus. Oh, and the non-skeuomorphic design, no matter it’s Material Design, Metro/ModernUI or Fluent Design, is just too ugly…
UPDATE 13–the Ramanujan Constant! This was an April Fools’ joke made in 1975 by Martin Gardner, who claimed that e^(π√163) was an integer, namely 262537412640768743. The idea was that most people were likely to be unable to get the actual result, which is 262537412640768743.99999999999925007259719818568887935…
But can we spot the hoax today, 44 years later?
- Android calculator: 2.625374126e17 (portrait) or 262537412640768743.9999999 (landscape)
- CalcTastic: 2.625374126408e17
- HiperCalc: 2.62537412640769e17 (as displayed) or 262537412640768743.99999999999925007259719818568887935… with 81 decimals
- ChampCalc: 262537412640768743.99999999999925007259 (as displayed) or up to 100 decimals
- Philip Stephens’: 2.62537412640768e17 (Approx. error: Ans – 262537412640768744 = 1024)
- TI-30X Pro: 2.625374126e17 (Approx. error: Ans – 262537412640768744 = 3000000)
- The 13 Vietnamese apps: 262537412640767712 (Approx. error: Ans – 262537412640768744 = -1032)
Only the Vietnamese pack were so confident as to display an exact integer with no scientific notation. And the worst precision was encountered in the physical TI-30X Pro device. But I was disappointed that I was unable to check CalcTastic’s internal error via “Ans – 262537412640768744”, as numbers longer than 13 digits can only be entered in the scientific notation!
BOTTOM LINE: while using a physical calculator (of the make and model of your choice) when and where appropriate, here’s what I recommend under Android to whoever can’t be satisfied with the stock calculator:
- ●●●●○ CalTastic‘s scientific calculator for everyday use. It’s responsive, practical, and good-looking. Free edition just fine. CONS: limited precision; I could not find how to edit previous inputs; unpractical conversions and statistics; not the best layout of buttons, e.g. square root and factorial as 2nd functions (a couple of years ago it was mimicking something else, and I kinda liked more the way the buttons were back then).
- ●●●○○ ChampCalc for everyday use when you need better precision or better aesthetics. Several themes. Free edition just fine. CONS: the buttons seem a bit slow to respond; the button layout seems good, but do we really need sign, mod and |x| as primary functions?
- ●●●●○ Philip Stephens‘ scientific calculator for advanced mathematics and engineering (e.g. integral calculus). The new generation (starting with version 9.3.0) has improved precision and is overall excellent for advanced calculus! CONS: “canonical” flat (material?) design; paid edition a bit expensive.
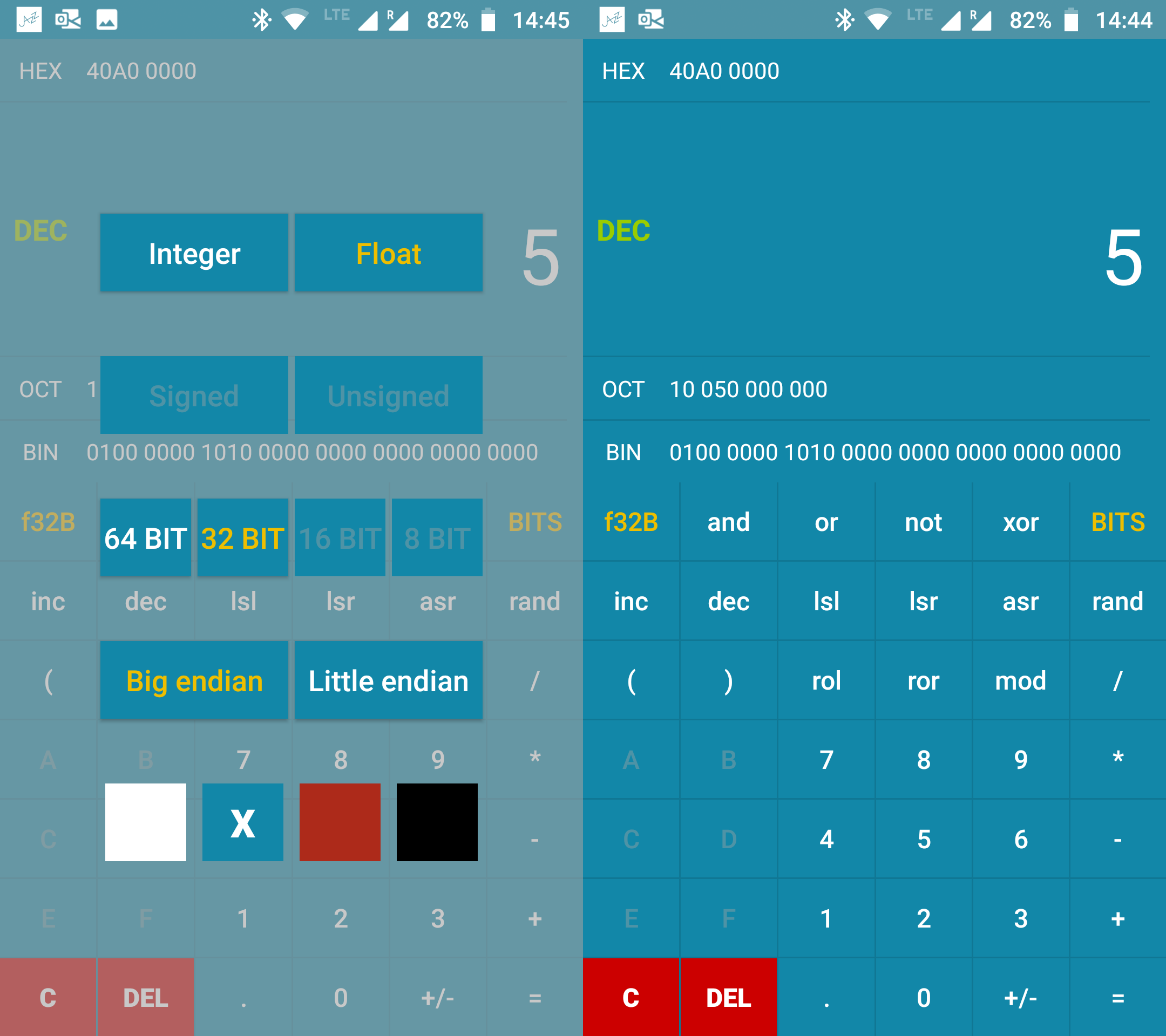
- ●●●●○ KebStudios’ Programmer’s calculator for operations in and between different bases. It supports binary-coded decimal, e.g. suppose you want to encode 5.0f on 32-bit as 0x40a00000 but you don’t know the hex value. Use the top-right button to reach the menu and change the integer to float, and f64B to f32B:
Screw the Vietnamese apps–all of them!
UPDATE to UPDATE 12: I’m stunned by how nonchalantly the Vietcong guy (sorry for the bad joke) releases new versions that don’t fix the random results any and all the 13 apps give to advanced calculus tasks! Here’s version 3.9.5-beta-24-03-2019-03-release of Calc Business, whose changelog includes “Improved calculate integral, limit, sum and product.”
The sum that should give 5.596796… still gives random results (different in decimal and fraction modes), and while it can sometimes compute an integral with discontinuity in zero, it generally fails the same as before:
Keep away from the Vietnamese calculators.
UPDATE to UPDATE to UPDATE 12: I just tested version 4.0.2-30-04-2019-16-release of “Calc Tavern” and it seems that almost all problems have been solved–all but the infinite loop mentioned at UPDATE 9. This doesn’t mean the Vietnamese calculators can be trusted. Note that the keyboard sound still mostly fails (it only happens randomly, once in a while), so vibration is the only feedback that can be trusted. This doesn’t make much sense, as typically the vibration is time-consuming and difficult to fine-tune, but don’t ask me to understand Vietnamese software…

Can you tell me if the Genie 92SC scientific calculator has power-off memory safeguard, so that when it turns off I can still scroll through the calculation history?
/Silicon Valley Regards
Unfortunately, I can’t tell, as I couldn’t find one in the department stores I checked. Unless I purchase one… online.
There is a thing about Genie 92SC: someone claims that when the display reads D, it actually means radians, and when it reads R it means degrees, which is dumb. I can’t tell though whether this is the case or not (ouch, there’s a second guy to mention the same issue).
Thanks for your reply.
Only the TI scientific calcs have memory safeguard. I don’t know why Casio has to delete its calculation history. After 7 minutes of non use, the expression you are working on is deleted when the Casio turns itself off, and you have to retype it, — a real pain if it’s a lengthy equation.
Both TI and Casio are allowed on exams in the U.S. but I like the features on the Casio better, especially the sexagesimal calculations; TI’s sexagesimal calculations are too clumsy and time-consuming. /Silicon Valley Regards
It’s a common complaint that Casio calculators don’t retain the last expressions; unfortunately, their lame user’s guides don’t mention this, just the fact that they’ll turn off after 6 minutes of non-use.
I was indeed surprised to see that TI-30X Plus MathPrint didn’t erase what I entered a couple of days ago 🙂
As for which devices are allowed in exams, each country has its own regulations (in Germany, each Land), but generally Casio and TI are what you’ll find in that list. That calculators are allowed in exams (although only specific devices, which is not always fair: your device might not be infringing any rule, e.g. if it can’t store alphanumeric strings, yet it would be banned if not specifically certified) is not a bad thing, but the fact that in some countries K-12 kids are sometimes required to purchase specific devices is totally unjust. How exactly are you teaching kids to simplify fractions if they’re doing it on a calculator?!
But I also have to say that I liked the screen of TI-30X Plus/Pro MathPrint: great contrast by default, and the typeface they chose renders some very nice digits! (BTW, Genie 92SC is said to have a poor contrast, like 30 years ago.)
The so-called UPDATE 11 is probably the 20th major edit. I give up.
Nope. UPDATE 12: new bugs and random results!
All 13 numbered updates aside, I’ve added a bottom line with a short list of apps.
Revisiting the Vietnamese calc apps (not to check whether each one is still there), I discovered a new one, by the same guy, no matter the displayed name: advanced.scientific.calculator.calc991.plus, by its name “Free scientific calculator es plus advanced 991 ex” by “Tools for student” (what a fucking ridiculous name!). It’s not free if you need e.g. integrals.
Most of the time I still use CalcTastic, despite the fact that, as a recent user review notes,
Yes. It’s not using arbitrary precision arithmetic. But the Vietcong one does:
Hello,
I’m the programmer of ChampCalc scientific calculator.
I really liked reading your professional review of my app, and I wanted to thank you.
I made many changes to improve the app, and I believe the current version (6.02 and above) is a mature and improved product.
Now, the math engine is fully supporting arbitrary precision (for free version also), and the calculator detects repeating decimal numbers (periodic numbers), and allows to edit them inside the expression.
The programmers calculator was also improved, and contains a full support of ‘Two’s Complement’.
I will be glad to get a re-review to continue to improve the product for all our users. I will also be glad to get from you tips for improvements in any field, mathematical or design.
Thanks!
Ben
Thanks for the feedback to the feedback 🙂
Speaking of suggestions, there are two issues with your app, as far as I am concerned:
1. The haptic and audio feedback is unpleasant. I can’t tell how to improve it, but the one I’m comfortable with is CalcTastic’s.
2. The rather peculiar position of some functions on the keyboard. I know, even in real life, Casio, Sharp, TI, HP don’t all use the same layouts, but under Android I’m already used to CalcTastic’s keyboard, and partially with the ones by Philip Stephens and by that Vietnamese guy. Somehow, I find yours a bit strange, w/o being able right now to point to the “strange” positions. Maybe you should aim to mimic a few popular Casio calculators.
Speaking of arbitrary precision, even with a precision of 50 digits, here’s what I got to the calculus for which you also have screenshots from two competitors (in my June 11 comment above):
Ouch.
Thank you so much for your comment!
Your professional feedbacks are very important to me, and allow me to create a better product for my users.
1. The haptic response (vibration and sound) is changeable in settings. I will try to check this case on other devices, and compare it to other apps.
2. The calculator offers lots of functions (all the buttons\secondaries are assigned). The functions are arranged according to some logical order, but I will check your point and consider making changes if it will be found relevant.
3. Currently, the parameter of the MOD function is limited to a maximum value of 1E40 (history reason), I will check the option to remove this limitation. The calculator handles very large numbers up to 1E99999 and this limitation can be changed too.
I know that the haptic response is configurable, but I just can’t find the right values. I’m very picky, and it’s difficult to replace physical buttons with a touchscreen 🙂
Concerning that integral from the Update 10 which android calculators fail to solve, and “to be able to compute on (-5, 99), but not on the sub-interval (0, 99)” part, it’s funny that Casio FX-991EX demonstrates the very same: it computes the integral on (-5,99) but instantly shows “Math ERROR” on (0,99).
P. S. By the way, the current version of HiPER Calc Pro (7.4.6) doesn’t have the wrong behavior described in the first lines of the Update 10, now it solves that integral well both in complex and in real modes. Still fails with the range from 0 to 99 though…
For the fun of it, here’s a calculus that doesn’t solve to an integer, even if it seems to:
One of the Vietnamese calculators (a new clone, this one) believes it’s an integer, and it even factorizes it!
The error is about 1032, not just 1e-13, so the Vietnamese apps, as I’ve already proven, exhibit absolutely random precision artifacts.
CalcTastic, as expected, can’t cope with such numbers with sufficient precision, but ChampCalc works like a charm:
The silicon-based errors are probably similar to CalcTastic’s (the internal representation has a better precision than displayed, but I didn’t investigate any further):